QL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QL
1
24 tháng 3 2018
a, ta có md là tia phân giác của góc M⇒
\(\dfrac{ND}{DP}=\dfrac{MN}{MP}=\dfrac{8}{12}\Rightarrow\dfrac{ND}{DP}=\dfrac{8}{12}=\dfrac{2}{3}\Rightarrow\dfrac{ND}{ND+DP}=\dfrac{2}{2+3}\Rightarrow\dfrac{ND}{NP}=\dfrac{2}{5}\)
13 tháng 9 2023
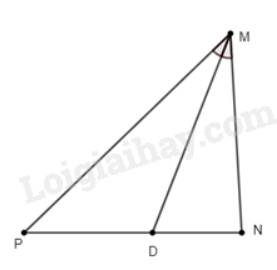
Vì \(MD\) là tia phân giác góc \(M\left( {D \in NP} \right)\) nên theo tính chất đường phân giác ta có:
\(\frac{{DN}}{{DP}} = \frac{{MN}}{{MP}};\frac{{DN}}{{MN}} = \frac{{DP}}{{MP}};\frac{{DP}}{{DN}} = \frac{{MP}}{{MN}};\frac{{DP}}{{MP}} = \frac{{DN}}{{MN}}\)
10 tháng 5 2022
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
Do đó: ΔHNM\(\sim\)ΔMNP
b: \(NP=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(MH=\dfrac{MN\cdot MP}{NP}=4.8\left(cm\right)\)
\(HN=\dfrac{MN^2}{NP}=3.6\left(cm\right)\)
=>HP=6,4(cm)
29 tháng 4 2020
a) Xét ΔMNP có MD là đường phân giác ứng với cạnh NP(gt)
nên \(\frac{ND}{NM}=\frac{DP}{PM}\)
\(\Leftrightarrow\frac{ND}{8}=\frac{7.5}{10}\)
hay \(ND=\frac{7.5\cdot8}{10}=\frac{60}{10}=6cm\)
Vậy: ND=6cm
b) Xét ΔMNP có DC//MP(gt)
nên \(\frac{NC}{CM}=\frac{ND}{DP}\)
\(\Leftrightarrow\frac{NC}{CM}=\frac{6}{7.5}\)
hay \(\frac{NC}{6}=\frac{CM}{7.5}\)
Ta có: NC+CM=MN=8cm(C nằm giữa N và M)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{NC}{6}=\frac{CM}{7.5}=\frac{NC+CM}{6+7.5}=\frac{NM}{13.5}=\frac{8}{13.5}=\frac{16}{27}\)
Do đó: \(\frac{NC}{6}=\frac{16}{27}\)
\(\Leftrightarrow NC=\frac{16\cdot6}{27}=\frac{96}{27}=\frac{32}{9}\simeq3.55cm\)
Vậy: NC\(\simeq\)3,55cm
a) \(\Delta MNP\)có \(MD\)là phân giác \(\widehat{M}\), áp dụng tính chất đường phân giác trong tam giác ta có:
\(\frac{DN}{MN}=\frac{DP}{MP}\) \(\Rightarrow\) \(\frac{DN}{DP}=\frac{MN}{MP}\)
hay \(\frac{DN}{DP}=\frac{8}{12}=\frac{2}{3}\)
b) \(\frac{DN}{DP}=\frac{2}{3}\)
hay \(\frac{6}{DP}=\frac{2}{3}\)
\(\Rightarrow\) \(DP=\frac{6.3}{2}=9\)