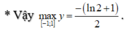Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Đặt $\sqrt[3]{1-x}=a; \sqrt[4]{1+x}=b$ thì bài toán trở thành:
Cho $a,b\geq 0$ thỏa mãn $a^4+b^4=2$
Tìm max $P=ab+a+b$
Thật vậy, áp dụng BĐT AM-GM:
$2=a^4+b^4\geq 2a^2b^2\Rightarrow ab\leq 1$
$a^4+b^4\geq \frac{1}{2}(a^2+b^2)^2$
$a^2+b^2\geq \frac{1}{2}(a+b)^2$
$\Rightarrow 2=a^4+b^4\geq \frac{(a+b)^4}{8}$
$\Rightarrow (a+b)^4\leq 16$
$\Rightarrow a+b\leq 2$
Do đó: $P=ab+a+b\leq 1+2=3$
Vậy $P_{\max}=3$ khi $a=b=1\Leftrightarrow x=0$

+ Xét hàm số f( x) = x3- x2+ ( m2+ 1) x- 4m- 7 trên đoạn [ 0; 2]
Ta có f’ (x) = 3x2- 2x+ m2+ 1= 3( x-1/3) 2+ m2+ 2/3> 0 .
+ Suy ra hàm số f(x) đồng biến trên
0 ; 2 ⇒ m i n [ 0 ; 2 ] f ( x ) = f ( 0 ) = - 4 m - 7 m a x [ 0 ; 2 ] f ( x ) = f ( 2 ) = 2 m 2 - 4 m - 1
+ Khi đó
m a x [ 0 ; 2 ] y = m a x [ 0 ; 2 ] f ( x ) = m a x - 4 m - 7 ; 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 4 m - 7 ≤ 15 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 11 2 ≤ m ≤ 2 2 m 2 - 4 m - 16 ≤ 0 ⇔ - 11 2 ≤ m ≤ 2 - 2 ≤ m ≤ 4 ⇔ - 2 ≤ m ≤ 2 → m ∈ ℤ m ∈ ± 2 ; ± 1 ; 0
Vậy có 5 giá trị thoả mãn.
Chọn C.

\(y=x+\dfrac{1}{x}-5\ge2\sqrt{x.\dfrac{1}{x}}-5=-3\)
Đáp án C

bạn trả lời từng câu cũng được mà :) làm được câu nào thì giúp mình nhé. Tks!

Chọn A
* Hàm số y = x - e 2 x xác định trên [-1;1]
* Ta có : ![]()
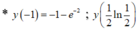
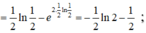
![]()