Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
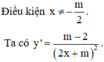
Hàm số đã cho đồng biến trên khoảng - ∞ ; - 8

Do đó, số tập con gồm 3 phần tử của tập hợp A là C 14 3 = 364

Ta có : \(\frac{8n+3}{2n-1}=4+\frac{7}{2n-1}\)
nên để \(8n+3\) chia hết cho \(2n-1\) thì \(7\)phải chia hết cho \(2n-1\), tức \(n\ne\frac{1}{2}\); \(n=1;n=4;\)
Vậy tập hơp các số nguyên thỏa mãn ycbt là \(n\in\left\{1;4\right\}\)
Để 8n + 3 chia hết cho 2n - 1 <=> \(\frac{8n+3}{2n-1}\) là số nguyên
Ta có :\(\frac{8n+3}{2n-1}=\frac{4\left(2n-1\right)+7}{2n-1}=\frac{4\left(2n-1\right)}{2n-1}+\frac{7}{2n-1}=4+\frac{7}{2n-1}\)
Để \(4+\frac{7}{2n-1}\) là số nguyên <=> \(\frac{7}{2n-1}\) là số nguyên
=> 2n - 1 \(\in\) Ư ( 7 ) => Ư ( 7 ) = { - 7 ; - 1 ; 1 ; 7 }
Ta có : 2n - 1 = - 7 <=> 2n = - 6 => n = - 3 ( TM )
2n - 1 = - 1 <=> 2n = 0 => n = 0 ( TM )
2n - 1 = 1 <=> 2n = 2 => n = 1 ( TM )
2n - 1 = 7 <=> 2n = 8 => n = 4 ( TM )
Vậy n \(\in\) { - 3 ; 0 ; 1 ; 4 }

vì 3n^2 chia hết cho 3 nên để A chia hết cho 3 thì ta CM
n^3+2n=n*(n*n+2) vì n là số nguyên nên n có dạng 3k; 3k+1;3k+2(k thuộc Z)
nếu n=3k thì n*(n*n+2) luôn luôn chia hết cho 3
nếu n=3k+1 thì n*n=(3k+1)*(3k+1)=9k^2+3k+3k+1 chia 3 dư 1 nên n*n+2 luôn luôn chia hết cho 3
nếu n=3k+2 thì n*n=(3k+2)*(3k+2)=9k^2+6k+6k+4 chia 3 dư 1 nên n*n+2 luôn luôn chia hết cho 3
vậy biểu thức trên luôn luôn chia hết cho 3 với mọi n thuộcZ
câu b)để A chia hết cho 15 thì n^3+3n^2+2n phải chia hết cho 3;5(vì ƯCLN(3;5)=1)
Mà theo câu a thì A luôn luôn chia hết cho 3 với n thuộc Z
nên ta chỉ cần tìm giá trị của n để A chia hết cho5
để A chia hết cho 5 thì n^3 phải chia hết cho 5;3n^2 phải chia hết cho 5;2n phải chia hết cho 5
nên n phải chia hết cho 5(vì ƯCLN(3;5)=1;ƯCLN(2;5)=1 nên n^3;n^2;n phải chia hết cho 5 nên ta suy ra n phải chia hết cho 5)
mà 1<n<10 nên n=5(n là số nguyên dương)
vậy giá trị của n thỏa mãn đề bài là 5

Đáp án A
Ta có 4 sin 2 x + 5 cos 2 x ≤ m . 7 cos 2 x ⇔ 4 1 - cos 2 x + 5 cos 2 x ≤ m . 7 cos 2 x ⇔ m ≥ 4 28 cos 2 x + 5 7 cos 2 x
Đặt t = cos 2 x , 0 ≤ t ≤ 1 khi đó m ≥ 4 28 t + 5 7 t = g t
Phương trình đã cho có nghiệm ⇔ m ≥ m i n 0 ; 1 g t
Dễ thấy g ' t < 0 ∀ t ∈ 0 ; 1 ⇒ m i n 0 ; 1 g t = g 1 = 6 7 ⇒ m ≥ 6 7 là giá trị cần tìm
Vậy a + b + c = 13.

Chọn B
Cách giải: Ta có:
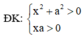
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
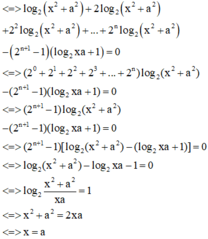
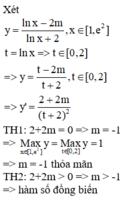
![]()





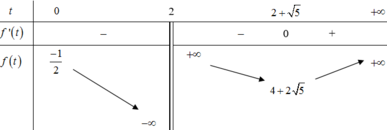

không biết giải
sorry nha !
chưa ai trả lời ngoài mình à ?