Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử z = x + yi (x, y ∈ R), khi đó số phức z được biểu diễn bởi điểm M(x, y) trên mặt phẳng tọa độ Oxy.
a) Trên hình 71.a (SGK), điểm biểu diễn ở phần gạch chéo có hoành độ có hoành độ x ≥ 1, tung độ y tùy ý.
Vậy số phức có phần thực lớn hơn hoặc bằng -1 có điểm biểu diễn ở hình 71.a (SGK)
b) Trên hình 71.b(SGK), điểm biểu diễn có tung độ y ∈ [1, 2], hoành độ x tùy ý.
Vậy số phức có phần ảo thuộc đoạn [-1, 2]
c) Trên hình 71.c (SGK), hình biểu diễn z có hoành độ x ∈ [-1, 1] và x2 + y2 ≤ 4 (vì |z| ≤ 4.
Vậy số phực có phần thực thuộc đoạn [-1, 1] và môdun không vượt quá 2.

\(\left(1-\dfrac{1}{2}\right)\):\(\left(1-\dfrac{1}{3}\right)\):\(\left(1-\dfrac{1}{4}\right)\):\(\left(1-\dfrac{1}{5}\right)\):\(\left(1-\dfrac{1}{6}\right)\):\(\left(1-\dfrac{1}{7}\right)\)
=\(\left(\dfrac{2-1}{2}\right)\):\(\left(\dfrac{3-1}{3}\right)\):\(\left(\dfrac{4-1}{4}\right)\):\(\left(\dfrac{5-1}{5}\right)\):\(\left(\dfrac{6-1}{6}\right)\)
=\(\dfrac{1}{2}\):\(\dfrac{2}{3}\):\(\dfrac{3}{4}\):\(\dfrac{4}{5}\):\(\dfrac{5}{6}\)
=\(\dfrac{1.\left(3.4.5\right)6}{\left(3.4.5\right)\left(2.2\right)}\)
=\(\dfrac{6}{2.2}=\dfrac{3}{2}\)

47. y=x ĐA: D
48. A(-4;0); B(0;4); C(x; 3)
\(\overrightarrow{AB}=\left(4;4\right);\overrightarrow{BC}=\left(x;-1\right)\)
A;B;C thẳng hàng\(\Rightarrow\dfrac{4}{x}=\dfrac{4}{-1}=>x=-1\) ĐA: D
49.A(2;-2); B(3;1); C(0;2)
\(\overrightarrow{AB}=\left(1;3\right);\overrightarrow{AC}=\left(-2;4\right);\overrightarrow{BC}\left(-3;1\right)\)
=>Tam giác vuông cân=> ĐA:C
51. ĐA:D
52: A(-1;3); B(-3;-2); C(4;1)
\(\overrightarrow{AB}=\left(-2;-5\right);\overrightarrow{AC}=\left(5,-2\right),\overrightarrow{BC}=\left(7;3\right)\)
ĐA: C

Em chỉ cần chú ý là bán \(\dfrac{1}{2}\) số còn lại mà đang còn dư 18 lít thì số còn lại sau khi bán một nửa là 36 lít. Từ đó suy ra cả thùng chưa bán có tất cả 72 lít


con hươu A nha,tick cho 1 cái đi,ko đúng ko tick cũng được nha

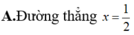
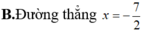
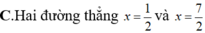
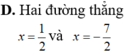




 mọi người giúp mình với
mọi người giúp mình với

Đáp án D.