Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(\frac{A}{2}+\left(\frac{B}{2}+\frac{C}{2}\right)=90^0\)
\(\Rightarrow sin\frac{A}{2}=cos\left(\frac{B}{2}+\frac{C}{2}\right)=cos\frac{B}{2}cos\frac{C}{2}-sin\frac{B}{2}.sin\frac{C}{2}\)
b/ \(\frac{tan^2A-tan^2B}{1-tan^2A.tan^2B}=\frac{\left(tanA-tanB\right)}{\left(1+tanA.tanB\right)}.\frac{\left(tanA+tanB\right)}{\left(1-tanA.tanB\right)}=tan\left(A-B\right).tan\left(A+B\right)\)
\(=tan\left(A-B\right).tan\left(180^0-C\right)=-tan\left(A-B\right).tanC\)
c/
\(A+B+C=180^0\Rightarrow cot\left(A+B\right)=-cotC\)
\(\Leftrightarrow\frac{cotA.cotB-1}{cotA+cotB}=-cotC\)
\(\Leftrightarrow cotA.cotB-1=-cotA.cotC-cotB.cotC\)
\(\Leftrightarrow cotA.cotB+cotB.cotC+cotA.cotC=1\)

phần chứng minh biểu thức không phụ thuộc \(x\)
ta có : \(A=\dfrac{cot^2a-cos^2a}{cot^2a}+\dfrac{sinacosa}{cota}=\dfrac{cot^2a-cos^2a}{cot^2a}+\dfrac{cos^2a}{cot^2a}\)
\(=\dfrac{cot^2a-cos^2a+cos^2a}{cot^2a}=\dfrac{cot^2a}{cot^2a}=1\left(đpcm\right)\)
ý còn lại : xem lại đề nha bn
phần chứng minh đẳng thức
ta có : \(\dfrac{sin2a-2sina}{sin2a+2sina}+tan^2\dfrac{a}{2}=\dfrac{2sinacosa-2sina}{2sinacosa+2sina}+tan^2\dfrac{a}{2}\)
\(=\dfrac{2sina\left(cosa-1\right)}{2sina\left(cosa+1\right)}+tan^2\dfrac{a}{2}=\dfrac{cosa-1}{cosa+1}+tan^2\dfrac{a}{2}\)
\(=\dfrac{1-2sin^2\dfrac{a}{2}-1}{2cos^2\dfrac{a}{2}-1+1}+tan^2\dfrac{a}{2}=\dfrac{-2sin^2\dfrac{a}{2}}{2cos^2\dfrac{a}{2}}+tan^2\dfrac{a}{2}\)
\(=-tan^2\dfrac{a}{2}+tan^2\dfrac{a}{2}=0\left(đpcm\right)\)
ta có : \(\dfrac{sina}{1+cosa}+\dfrac{1+cosa}{sina}=\dfrac{sin^2a+\left(1+cosa\right)^2}{sina\left(1+cosa\right)}\)
\(=\dfrac{sin^2a+cos^2a+2cosa+1}{sina\left(1+cosa\right)}=\dfrac{2cosa+2}{sina\left(cosa+1\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(cosa+1\right)}=\dfrac{2}{sina}\left(đpcm\right)\)
còn 2 câu kia để chừng nào rảnh mk giải cho nha
mk lm 2 câu còn lại nha
ta có : \(\dfrac{sin^2x}{sinx-cosx}-\dfrac{sinx+cosx}{tan^2x-1}=\dfrac{\left(1-cos^2x\right)\left(tan^2x-1\right)-\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}\)
\(=\dfrac{tan^2x-sin^2x-sin^2x-sin^2x+cos^2x}{\left(sinx-cosx\right)\left(tan^2x-1\right)}=\dfrac{\dfrac{sin^4x}{cos^2x}-sin^2x-sin^2x+cos^2x}{\left(sinx-cosx\right)\left(tan^2-1\right)}\)
\(=\dfrac{tan^2x\left(sin^2x-cos^2x\right)-\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}=\dfrac{\left(tan^2x-1\right)\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}\)
\(=sinx+cosx\left(đpcm\right)\)
ta có : \(\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{1-tan^2a.cot^2b}=\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{1-\dfrac{sin^2a.cos^2b}{cos^2a.sin^2b}}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{\dfrac{cos^2a.sin^2b-sin^2a.cos^2b}{cos^2a.sin^2b}}=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-\left(sin^2a.cos^2b-cos^2a.sin^2b\right)}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-\left(\left(sina.cosb-cosa.sinb\right)\left(sina.cosb+cosa.sinb\right)\right)}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-sin\left(a-b\right)sin\left(a+b\right)}=-cos^2a.sin^2b\left(đpcm\right)\)
mk lm hơi tắc ! do tối rồi , mà mk lại đang ở quán nek nên không tiện làm dài . bạn thông cảm

\(A+B+C=180^0\Rightarrow tan\left(A+B\right)=-tanC\)
\(\Rightarrow\frac{tanA+tanB}{1-tanA.tanB}=-tanC\Leftrightarrow tanA+tanB=-tanC+tanA.tanB.tanC\)
\(\Leftrightarrow tanA+tanB+tanC=tanA.tanB.tanC\)
\(2A+2B+2C=360^0\Rightarrow tan\left(2A+2B\right)=-tan2C\)
\(\Leftrightarrow\frac{tan2A+tan2B}{1-tan2A.tan2B}=-tan2C\)
\(\Leftrightarrow tan2A+tan2B+tan2C=tan2A.tan2B.tan2C\)

Câu a)
Ta sử dụng 2 công thức:
\(\bullet \tan (180-\alpha)=-\tan \alpha\)
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha.\tan \beta}\)
Áp dụng vào bài toán:
\(\text{VT}=\tan A+\tan B+\tan C=\tan A+\tan B+\tan (180-A-B)\)
\(=\tan A+\tan B-\tan (A+B)=\tan A+\tan B-\frac{\tan A+\tan B}{1-\tan A.\tan B}\)
\(=(\tan A+\tan B)\left(1+\frac{1}{1-\tan A.\tan B}\right)=(\tan A+\tan B).\frac{-\tan A.\tan B}{1-\tan A.\tan B}\)
\(=-\tan A.\tan B.\frac{\tan A+\tan B}{1-\tan A.\tan B}=-\tan A.\tan B.\tan (A+B)\)
\(=\tan A.\tan B.\tan (180-A-B)\)
\(=\tan A.\tan B.\tan C=\text{VP}\)
Do đó ta có đpcm
Tam giác $ABC$ có ba góc nhọn nên \(\tan A, \tan B, \tan C>0\)
Áp dụng BĐT Cauchy ta có:
\(P=\tan A+\tan B+\tan C\geq 3\sqrt[3]{\tan A.\tan B.\tan C}\)
\(\Leftrightarrow P=\tan A+\tan B+\tan C\geq 3\sqrt[3]{\tan A+\tan B+\tan C}\)
\(\Rightarrow P\geq 3\sqrt[3]{P}\)
\(\Rightarrow P^3\geq 27P\Leftrightarrow P(P^2-27)\geq 0\)
\(\Rightarrow P^2-27\geq 0\Rightarrow P\geq 3\sqrt{3}\)
Vậy \(P_{\min}=3\sqrt{3}\). Dấu bằng xảy ra khi \(\angle A=\angle B=\angle C=60^0\)
Câu b)
Ta sử dụng 2 công thức chính:
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha.\tan \beta}\)
\(\bullet \tan (90-\alpha)=\frac{1}{\tan \alpha}\)
Áp dụng vào bài toán:
\(\text{VT}=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{B}{2}.\tan \frac{C}{2}+\tan \frac{C}{2}.\tan \frac{A}{2}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{C}{2}(\tan \frac{A}{2}+\tan \frac{B}{2})\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan (90-\frac{A+B}{2})(\tan \frac{A}{2}+\tan \frac{B}{2})\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{\tan (\frac{A+B}{2})}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{1-\tan \frac{A}{2}.\tan \frac{B}{2}}}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+1-\tan \frac{A}{2}.\tan \frac{B}{2}=1=\text{VP}\)
Ta có đpcm.
Cũng giống phần a, ta biết do ABC là tam giác nhọn nên
\(\tan A, \tan B, \tan C>0\)
Đặt \(\tan A=x, \tan B=y, \tan C=z\). Ta có: \(xy+yz+xz=1\)
Và \(T=x+y+z\)
\(\Rightarrow T^2=x^2+y^2+z^2+2(xy+yz+xz)\)
Theo hệ quả quen thuộc của BĐT Cauchy:
\(x^2+y^2+z^2\geq xy+yz+xz\)
\(\Rightarrow T^2\geq 3(xy+yz+xz)=3\)
\(\Rightarrow T\geq \sqrt{3}\Leftrightarrow T_{\min}=\sqrt{3}\)
Dấu bằng xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}\Leftrightarrow \angle A=\angle B=\angle C=60^0\)

\(\dfrac{A}{2}+\dfrac{B}{2}=\dfrac{\pi}{2}-\dfrac{C}{2}\Rightarrow tan\left(\dfrac{A}{2}+\dfrac{B}{2}\right)=tan\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)\)
\(\Rightarrow\dfrac{tan\dfrac{A}{2}+tan\dfrac{B}{2}}{1-tan\dfrac{A}{2}tan\dfrac{B}{2}}=cot\dfrac{C}{2}=\dfrac{1}{tan\dfrac{C}{2}}\)
\(\Rightarrow tan\dfrac{A}{2}.tan\dfrac{C}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}=1-tan\dfrac{A}{2}tan\dfrac{B}{2}\)
\(\Rightarrow tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}=1\)
Ta có:
\(tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\ge\sqrt{3\left(tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}\right)}=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(A=B=C\) hay tam giác ABC đều
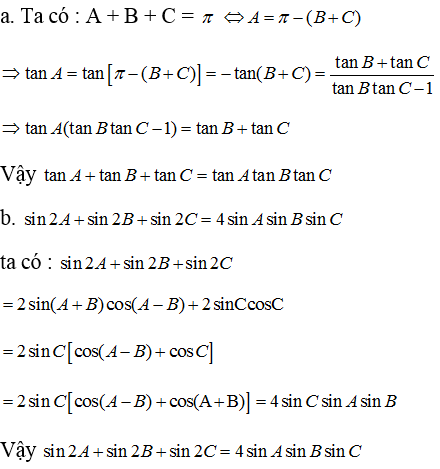


cao nhân đi qua giúp em với, mai thầy kiểm tra rồi hiccc
sao kh tag được như trước nữa nhỉ :((