Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

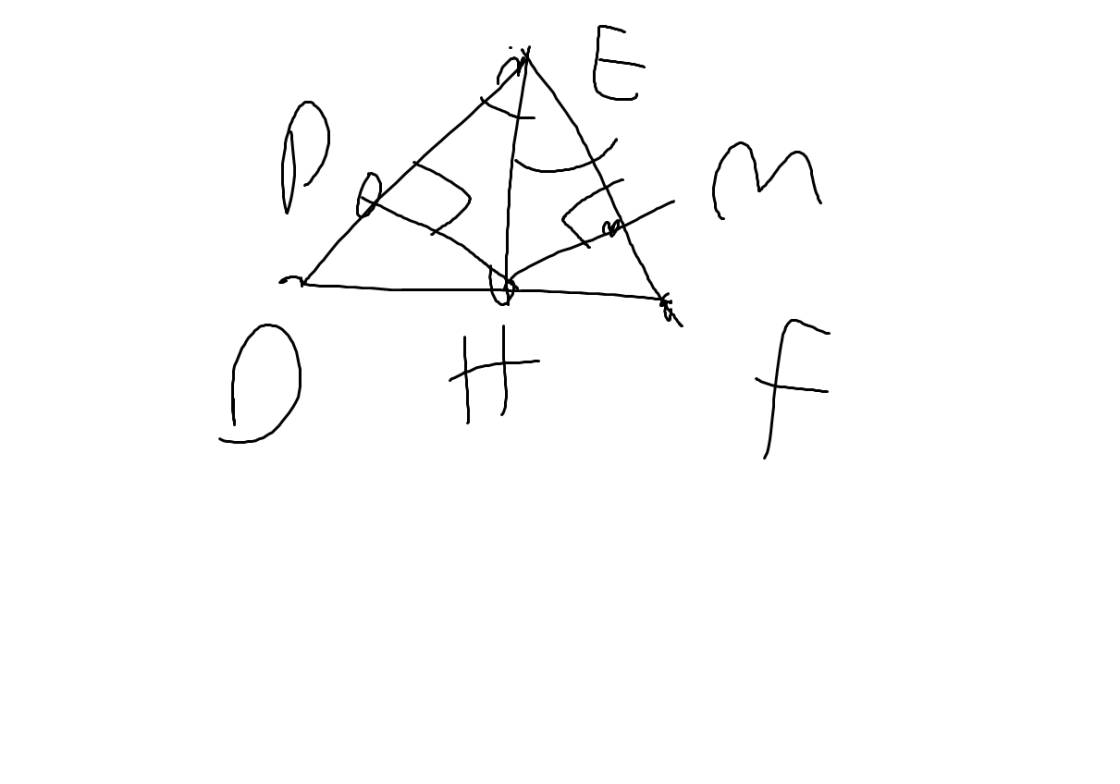
a: Xét ΔEFG cân tại E có EH là đường phân giác
nên H là trung điểm của FG
hay HF=HG
b: Ta có: ΔEFG cân tại E
mà EH là đường trung tuyến
nên EH là đường cao

Xét ΔJHF vuông tại H và ΔKIG vuông tại I có
HF=IG
góc JFH=góc KGI
=>ΔJHF=ΔKIG
=>HF=IG
Xét tứ giác JHKI có
JH//KI
JH=KI
=>JHKI là hình bình hành
=>HL=LI
FH+LG=IG+LQ=IL=HL

a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔABE=ΔHBE
b: Ta có:ΔABE=ΔHBE
nên BA=BH và EA=EH
=>BE là đường trung trực của AH
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: EK=EC
hay ΔEKC cân tại E
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC

a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)

Hệ thức lượng:
\(\Delta FEG\left(\widehat{F}=90^o\right)\) có:
\(\frac{1}{FH^2}=\frac{1}{FG^2}+\frac{1}{FI^2}\Leftrightarrow\frac{1}{FH^2}=\frac{1}{16^2}+\frac{1}{12^2}\Leftrightarrow FH=9,6\)

Xét ΔEAB co
BH,AD là đường cao
BH cắt AD tại H
=>H là trực tâm
=>EH vuông góc AB
=>EH//CA
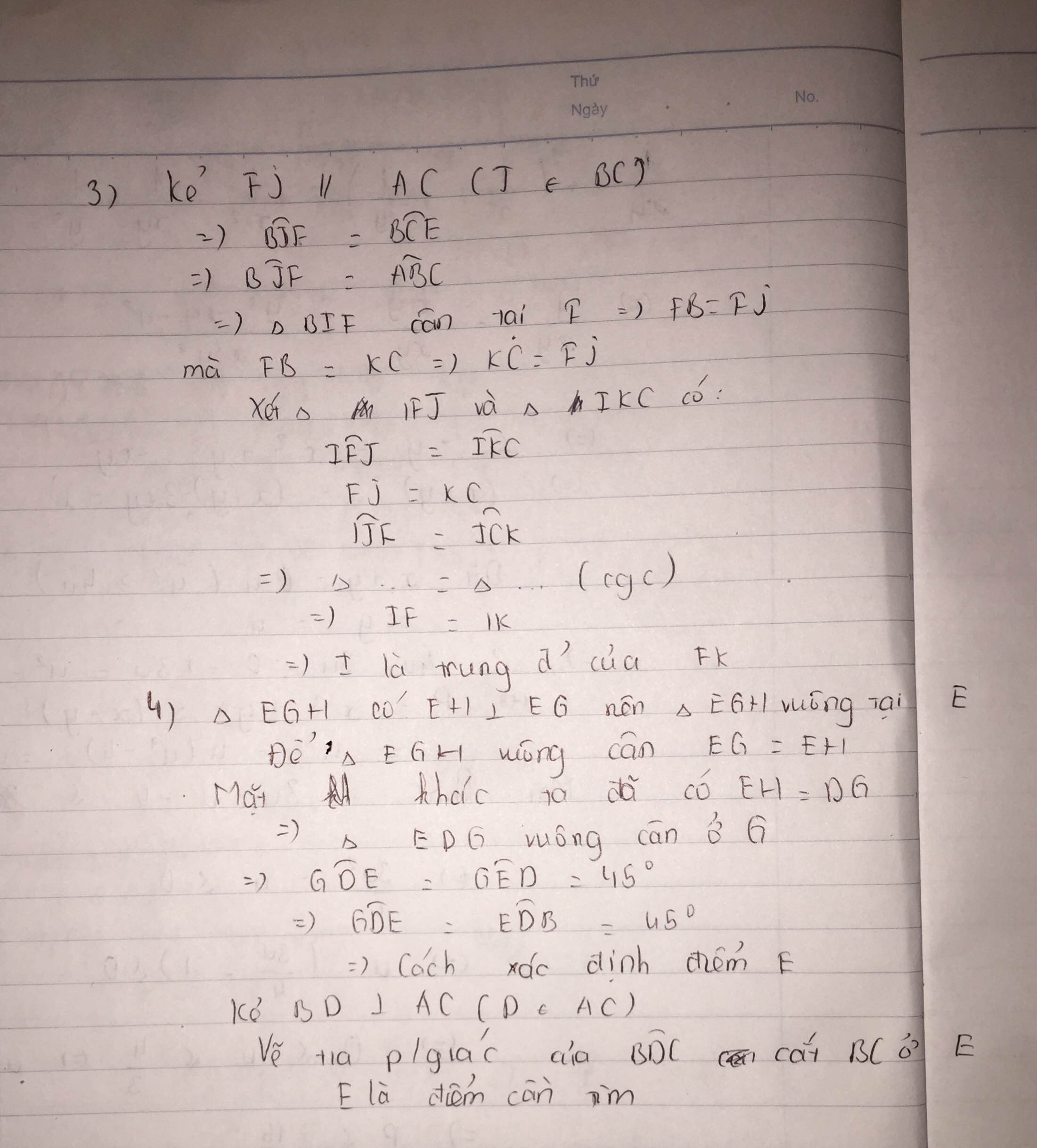
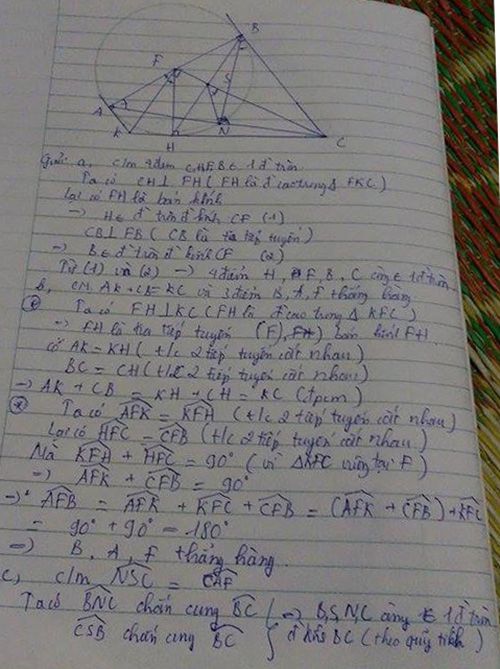 CÓ PHẢI KO
CÓ PHẢI KO
Hình tự vẽ !~ Vì \(\Delta EFG\) vuông tại E \(\Rightarrow\widehat{E}=90^0\)
Xét \(\Delta EFG\) có \(\widehat{E}=90^0\Rightarrow EF^2+EG^2=FG^2\left(ĐLPytago\right)\)
\(\Rightarrow EG^2=FG^2-EF^2=20^2-12^2=400-144=256=16^2\Rightarrow EG=16\left(cm\right)\)
Có diện tích tam giác ABC : \(S_{ABC}=\frac{1}{2}EF.EG=\frac{1}{2}EH.FG\)
\(\Rightarrow EF.EG=EH.FG\Leftrightarrow EH=\frac{EF.EG}{FG}=\frac{12.16}{20}=9,6\left(cm\right)\)