Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác BAM cân tại B ( BM=BA ); tam giác CAN cân tại C => Góc AMN = (180 độ - B):2; Góc ANM = (180-C):2
Góc AMN + Góc CAN = (360-(B+C))/2=(360-90)/2=135
Xét tam giác AMN có góc MAN = 180 - ( Góc AMN + Góc CAN) = 180 -135 =45
Chúc bạn học giỏi ;)

A B C M N
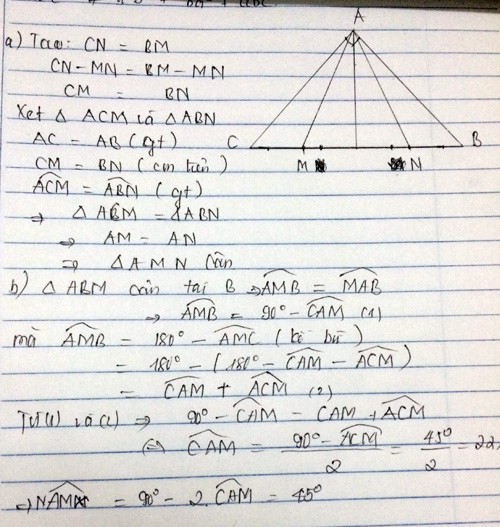
Ta có
BM=AB suy ra tam giác BAM cân tại B suy ra \(\widehat{BAM}=\frac{180^o-\widehat{B}}{2}\)
CN=AC suy ra tam giác NAC cân tại C suy ra \(\widehat{NAC}=\frac{180^o-\widehat{C}}{2}\)
(nếu cần thì bạn phải cm thêm cả N nằm giữa B và M nhé!)
MÀ ta thấy \(\widehat{BAM}+\widehat{ACN}=\widehat{BAC}+\widehat{NAM}\)
\(\Rightarrow\frac{180^o-\widehat{B}}{2}+\frac{180^o-\widehat{C}}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-90^o}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\widehat{NAM}=45^o\)

A B C M N 1 2 3 1 1
xet tam giac ABM can tai B co ^A1= ^BAM - ^A2
va ^M1= \(\frac{180-B}{2}\); ^BAM= ^M1
xet tam giac ACN can tai C co ^A3= ^NAC - ^A2
va ^N1=\(\frac{180-C}{2}\); ^NAC= ^N1
ta co ^A1 + ^ A2 + ^ A3 =90
^A2+ ^BAM - ^A2 +^NAC - ^A2 =90
^N1 + ^M1 =90+ ^A2
\(\frac{180-B}{2}\)+\(\frac{180-C}{2}\)=90+ ^A2
\(\frac{360-\left(B+C\right)}{2}=90+A2\)
\(\frac{360-90}{2}=90+A2\)
=> ^A2=45


A B C H M N K D E = = x x
| GT | △ABC cân tại A. BM ⊥ AC, CN ⊥ AB. BM ∩ CN = {K}. AK ∩ BC = {H}. MD = MK ; NE = NK |
KL | a. BM = CN b, AK là p/g BAC c, AK ⊥ BC d, △AED cân |
Bài giải:
a, Xét △BMA vuông tại M và △CNA vuông tại N
Có: AB = AC (△ABC cân tại A)
BAC là góc chung
=> △BMA = △CNA (ch-gn)
=> BM = CN (2 cạnh tương ứng)
b, Xét △NKA vuông tại N và △MKA vuông tại M
Có: AN = AM (△BMA = △CNA)
AK là cạnh chung
=> △NKA = △MKA (ch-cgv)
=> NAK = MAK (2 góc tương ứng) (1)
Và AK nằm giữa AN và AM
Mà N 

=> AK nằm giữa AB và AC (2)
Từ (1) và (2)
=> AK là phân giác BAC
c, Xét △BAH và △CAH
Có: BA = CA (cmt)
BAH = CAH (cmt)
AH là cạnh chung
=> △BAH = △CAH (c.g.c)
=> BHA = CHA (2 góc tương ứng)
Mà BHA + CHA = 180o (2 góc kề bù)
=> BHA = CHA = 180o : 2 = 90o
=> AH ⊥ BC
Mà AK ∩ BC = {H}
=> AK ⊥ BC
d, Xét △NEA vuông tại N và △NKA vuông tại N
Có: NE = NK (gt)
AN là cạnh chung
=> △NEA = △NKA (2cgv)
=> AE = AK (2 cạnh tương ứng)
Xét △DMA vuông tại M và △KMA vuông tại M
Có: MD = MK (gt)
AM là cạnh chung
=> △DMA = △KMA (2cgv)
=> AD = AK (2 cạnh tương ứng)
Mà AE = AK (cmt)
=> AD = AE
Xét △ADE có: AD = AE (cmt) => △ADE cân tại A

a, ta có : tam giác ABC có A=90o => tam giác ABC là tam giác vuông
Áp dụng định lí py-ta-go trong tam giác ABC ta có :
AB2+AC2=BC2
mà AB=6cm ; AC=8cm
=> 62+82=BC2
BC2=100
=> BC=10 cm
vì cac duong trung tuyen BN;CP cat nhau tai G ( N c AC ; P c AB)
=> BP=PA=3cm ; AN=NC=4cm
Áp dụng định lí py-ta-go trong tam giác vuông PAC và tam giác vuông BAN ta có :
tam giác PAC : tam giác BAN
BN2=BA2+AN2 CP2=AP2+AC2
mà BA=6 cm ;AC=8cm ; AN=4cm ;AP=3cm
=>BN2=62+42 CP2=32+82
=> BN2=52 CP2=73
=>BN=căn 52 CP=căn 73
30 độ ak
mk làm đc rồi