Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có độ dài của các cạnh tam giác ABC rồi mà đáng lẽ phải tính các cạnh của tam giác A'B'C' chứ ????
Tự vẽ hình nha :"))))
Ta có tam giác ABC đồng dạng với tam giác A'B'C'
\(\Rightarrow\frac{S_{ABC}}{S_{A'B'C'}}=\left(\frac{AB}{A'B'}\right)^2\)
Mà tam giác ABC có độ dài các cạnh là 3,4,5 nên là tam giác vuông
\(\Rightarrow S_{ABC}=\frac{1}{2}.3.4=6\left(cm^2\right)\)
\(\Rightarrow\frac{6}{54}=\left(\frac{AB}{A'B'}\right)^2\Rightarrow\left(\frac{AB}{A'B'}\right)^2=\frac{1}{9}\Rightarrow\frac{AB}{A'B'}=\frac{1}{3}\)
\(\Rightarrow A'B'=3.AB=3.3\)
Nên mỗi cạnh của tam giác A'B'C' gấp 3 lần của cạnh của tam giác ABC.
Suy ra ba cạnh của tam giác A'B'C là 9cm, 12cm, 15cm
A A' B B' C C'
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng
\(S=\frac{1}{2}.AB.AC=6\left(cm^2\right)\)
\(\Delta ABC~\Delta A'B'C'\left(gt\right)\)
\(\Rightarrow\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k\)
( với k là tỉ số đồng dạng ).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
\(\Rightarrow k^2=\frac{S_{A'B'C'}}{S_{ABC}}=\frac{54}{6}=9\Rightarrow k=3\)
\(\Rightarrow A'B'=3.AB=3.3=9\left(cm\right)\)
\(B'C'=3.BC=3.5=15\left(cm\right)\)
\(C'A'=3.CA=3.4=12\left(cm\right)\)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.

Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’ 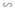 ΔABC ⇒
ΔABC ⇒ 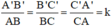
Áp dụng tính chất dãy tỉ số bằng nhau ta có:

∆ABC ∽ ∆A'B'C' => ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′ = CABCCA′B′C′CABCCA′B′C′
hay 3A′B′3A′B′ = 7B′C′7B′C′ = 5A′C′5A′C′ = CABC55CABC55 = 311311
=> A'B' = 11cm;
B'C' = 7.1137.113 ≈ 25.67 cm
A'C' = 5.1135.113 ≈ 18,33 cm

Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).

Anh mình nghĩ là như thế này. Mà ko biết đúng hay sai .
Ta có : \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
Suy ra : \(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow B'C'=\frac{5.4,5}{3}=7,5\)
\(C'A'=\frac{7.4,5}{3}=10,5\)
Chu vi tam giác A'B'C' là :
4,5 + 7,5 + 10,5 = 22,5 cm
Đ/s : 22,5 cm

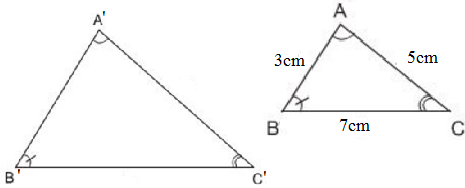
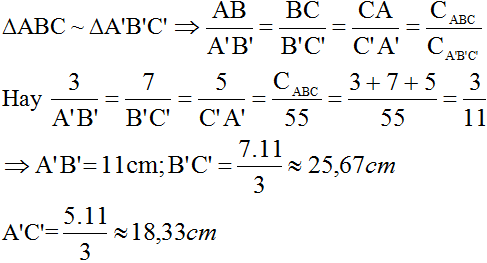
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.