Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
Ta có: 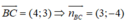
Đường thẳng BC đi qua B và có vecto 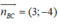 là vecto pháp tuyến:
là vecto pháp tuyến:
BC: 3(x + 1) - 4(y - 0) = 0 ⇔ 3x - 4y + 3 = 0
Gọi AH là đường cao của tam giác ABC
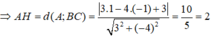

A B C I S D E F G K L K' M x
Gọi giao điểm khác D của hai đường tròn (BED);(CFD) là K'; K'I cắt EF tại L; DL cắt (I;ID) tại M khác D.
Ta thấy IE = IF; AI là phân giác ngoài của ^EAF, từ đây dễ suy ra 4 điểm A,E,I,F cùng thuộc một đường tròn
Vì 3 điểm D,F,E lần lượt thuộc các cạnh BC,CA,AB của \(\Delta\)ABC nên (BED);(CFD);(AFE) đồng quy (ĐL Miquel)
Hay điểm K' thuộc đường tròn (AIFE). Do vậy LI.LK' = LE.LF = LD.LM (= PL/(G) = PL/(I) )
Suy ra 4 điểm K',M,I,D cùng thuộc một đường tròn. Mà ID = IM nên ^IK'D = ^IK'M.
Đồng thời ^DIM = 1800 - ^DK'M = 1800 - ^EK'F + 2.^FK'D = ^BAC + 2.^ACB = 2.^AID
Suy ra IA vuông góc DM, từ đó M,L,D,A thẳng hàng (Vì IA cũng vuông góc AD)
Khi đó dễ thấy AL là phân giác ^BAC, K'L là phân giác ^EK'F, mà tứ giác AEK'F nội tiếp
Suy ra AEK'F là tứ giác điều hòa, từ đây AK' là đường đối trung của \(\Delta\)AEF
Suy ra K' trùng K. Kẻ tiếp tuyến Kx của (G), ta có ^BKx = ^EKx - ^EKB = ^EFK - ^EFD = ^BCK
Do đó (BKC) tiếp xúc với (G) tại K, tức KG đi qua tâm của (BKC) (1)
Gọi S là trung điểm cung lớn BC của (ABC). Có SB = SC và ^BKC = ^AED + ^AFD = 1800 - ^BSC/2
Suy ra S là tâm của đường tròn (BKC) (2)
Từ (1) và (2) suy ra KG luôn đi qua S cố định (Vì S là trung điểm cùng BC lớn cố định) (đpcm).

∞ Xét ▲ABK và ▲ACH có :
Góc A chung
Góc E = Góc D = 1v
AB = AC ( ▲ABC cân tại A )
Nên ▲ABK = ▲ACH (chgn) → AH = AK
∞ Xét ▲ADH và ▲ADK có :
AD chung
Góc H = Góc K = 1v
AH = AK (cmt)
Nên ▲ADH = ▲ADK (chcgv) → \(A_1=A_2\) kết hợp với AD nằm giữa AB và AC → AD phân giác góc A mà trong tam giác cân phân giác cũng là đường cao nên AD là đường cao hay BD _|_ AC.
CHÚC BẠN HỌC TỐT !!!
A B C D H K 1 2

4 cách phát biểu mệnh đề \(P \Leftrightarrow Q\):
“Tam giác ABC cân tương đương nó có hai đường cao bằng nhau”
“Tam giác ABC cân là điều kiện cần và đủ để nó có hai đường cao bằng nhau”
“Tam giác ABC cân khi và chỉ khi nó có hai đường cao bằng nhau”
“Tam giác ABC cân nếu và chỉ nếu nó có hai đường cao bằng nhau”

a.
Gọi (D):y=ax+b chứa điểm A, C
(D'):y=a'x+b' chứa điểm B, C
* Ta có: A thuộc (D) khi 1= 2a+b (1)
C thuộc (D) khi 4= 3a+b (2)
Giải hệ (1), (2) ta suy ra a=3 , b=-5
* Ta có: B thuộc (D') khi 3=6a'+b' (3)
C thuộc (D') khi 4=3a'+b' (4)
Giải hệ (3), (4) ta suy ra a=-1/3 , b= 5
Ta thấy: a.a' = 3.(-1/3)=-1
Suy ra (D) vuông góc (D') tại điểm chung C của của 2 cạnh (5)
Vậy tam giác ABC vuông tại C
Theo công thức tính cạnh của đoạn thẳng trong hệ trục tọa độ ta có:
AC=\(\sqrt{\left(x_A-x_C\right)^2+\left(y_A-y_C\right)^2}=\sqrt{\left(2-3\right)^2+\left(1-4\right)^2}\)\(=\sqrt{10}\)
BC=\(\sqrt{\left(x_B-x_C\right)^2+\left(y_B-y_C\right)^2}=\sqrt{\left(6-3\right)^2+\left(3-4\right)^2}\)\(=\sqrt{10}\)
Vậy AC=BC (6)
Từ (5) và (6) ta suy ra tam giác ABC vuông cân tại C
SABC=\(\dfrac{1}{2}\).AB.BC=\(\dfrac{1}{2}.\sqrt{10}.\sqrt{10}=\dfrac{1}{2}.10=\)5 (đvdt)
b. Làm tương tự câu a tìm độ dài các cạnh AB, BD, DA và tính diện tích bằng công thức SABD=\(\sqrt{p\left(p-AB\right)\left(p-BD\right)\left(p-DA\right)}\) với p là nửa chu vi tam giác ABD \(p=\dfrac{1}{2}\left(AB+BD+DA\right)\)
Tiếp tục dùng công thức SABD=\(=\dfrac{1}{2}.AB.BD.sinB\) các số liệu nêu trên đã có, chỉ cần thế vào là có góc B
Gọi I là tâm. Tìm độ dài bán kình bằng công thức SABD=\(\dfrac{AB.BD.DA}{4AI}\)
ta tìm được độ dài AI còn cách xác định tâm thì dựa vào giao điểm 2 đường thẳng (d) chứa đoạn AI và (d') chứa đoạn BI là xong

\(AB=\sqrt{\left(-2-2\right)^2+\left(-1+2\right)^2}=\sqrt{17}\)
\(AC=\sqrt{\left(1-2\right)^2+\left(2+2\right)^2}=\sqrt{17}\)
Vậy tam giác ABC cân tại A.

\(\dfrac{b^2-a^2}{2c}=b.\dfrac{\left(b^2+c^2-a^2\right)}{2bc}-a.\dfrac{\left(a^2+c^2-b^2\right)}{2ac}\)
\(\Leftrightarrow\dfrac{b^2-a^2}{2c}=\dfrac{b^2+c^2-a^2}{2c}-\dfrac{a^2+c^2-b^2}{2c}\)
\(\Leftrightarrow b^2-a^2=\left(b^2+c^2-a^2\right)-\left(a^2+c^2-b^2\right)\)
\(\Leftrightarrow3b^2=3a^2\Leftrightarrow a=b\)
Hay tam giác cân tại C

a: \(\overrightarrow{AB}=\left(-4;2\right)\)
\(\overrightarrow{BC}=\left(6;-3\right)\)
Vì \(\overrightarrow{BA}\cdot\overrightarrow{BC}=\overrightarrow{0}\) nên ΔABC vuông tại B
