K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LV
2

28 tháng 7 2016
Khi mức cường độ âm tăng thêm 10n (dB) thì cường độ âm tăng thêm 10^n lần.
CM:
10lg(I2/I0) - 10lg(I1/I0) = 10n
=> lg(I2/I0) - lg(I1/I0) = n
=> lg(I2/I1) = n
=> I2/I1 = 10^n
=> I2 = 10^n.I1
Vậy khi mức cường độ âm nào đó tăng thêm 30dB thì cường độ của âm tăng lên 1000 lần.
Vậy B đúng
SS
28 tháng 7 2016
\(L=10log\frac{I}{I_0}\) Khi I tăng 1000 = 103 lần \(\Rightarrow\) L tăng 30 db
chọn B

24 tháng 7 2016
Công thức tính mức cường độ âm là:
\(L=lg\frac{I}{I_0}=lg100=2B\) = 20 dB
SS
24 tháng 7 2016
Áp dụng công thức tính mức cường độ âm:
\(L\left(dB\right)=10.lg\frac{I}{I_0}=20dB\)

19 tháng 8 2016
Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng
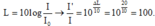
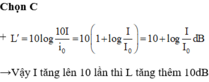


Đáp án: C
HD Giải: