Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có:
![]()
Bước sóng:
![]() cm
cm
Kết hợp với:
![]()
Biên độ cực tiểu
![]()
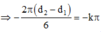 ( k lẻ)
( k lẻ)
![]()
Mặc khác
![]()
![]()
vì k lẻ nên có 2 giá trị thỏa mãn.
Có 2 điểm dao động với biên độ cực tiểu trên CD

Đáp án C
- Phương trình sóng tại điểm M do nguồn A và nguồn B truyền tới:
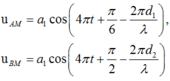
- Biên độ sóng tổng hợp tại M:
![]()
- Biên độ sóng tổng hợp tại M đạt giá trị cực tiểu khi:
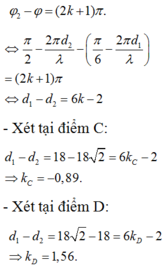
Vậy: Có hai điểm dao động với biên độ cực tiểu trên đoạn CD.

Chọn D
Hai nguồn A, B cùng pha
ðĐể giữa hai điểm CD có cực đại thì giữa A và B cũng chỉ có đúng 3 đường cực đại thì k nhận các giá trị -1,0,1. Nghĩa là phải có vân cực đại bậc 1 vân bậc 2 phải nằm ngoài.
ðCA-CB£kl£DA-DB
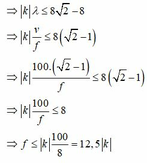
=> với k =1 thì f=12,5Hz
Với k=2 thì f=25Hz
=> phải nhỏ hơn 25Hz để không có vân bậc 2 trong khoảng CD và f phải lớn hơn hoặc bằng 12,5 Hz để có đủ 3 vân cực đại.

Ta thấy trên nửa đường thẳng thẳng kẻ từ A và vuông góc với AB có 4 điểm theo thứ tự M, N, P, Q dao động với biên độ cực đại, nên trên AB có 9 điểm dao động với biên độ cực đai với - 4 ≤ k ≤ 4 ( d2 – d1 = kλ)
A B x M N P Q
Cực đại tại M, N, P, Q ứng với k = 1; 2; 3; 4
Đặt AB = a
Tại C trên Ax là điểm dao động với biên độ cực đại:
CB – CA = kλ (*)
CB2 – CA2 = a2 → (CB + CA) (CB – CA) = a2
CB + CA = \(\dfrac{a^2}{k.\lambda}\)(**)
Từ (*) và (**) suy ra \(CA=\dfrac{a^2}{2k.\lambda}-\dfrac{k}{2}\lambda\)
Tại M: ứng với k = 1: MA = \(\dfrac{a^2}{2\lambda}\)- 0,5λ (1)
Tại N: ứng với k = 2: NA = \(\dfrac{a^2}{4\lambda}\)- λ (2)
Tại P: ứng với k = 3: PA = \(\dfrac{a^2}{6\lambda}\) - 1,5 λ (3)
Tại Q: ứng với k = 4: QA = \(\dfrac{a^2}{8\lambda}\) - 2 λ (4)
Lấy (1) – (2) : MN = MA – NA = \(\dfrac{a^2}{4\lambda}\) + 0,5λ = 22,25 cm (5)
Lấy (2) – (3) : NP = NA – PA = \(\dfrac{a^2}{12\lambda}\) + 0,5λ = 8,75 cm (6)
Lấy (5) - (6) → \(\dfrac{a^2}{\lambda}\) = 81 (cm) và λ = 4 cm .
Thế vào (4) → QA = 2,125 cm.
thầy có thể giải thích e chổ CB-CA= Klamda . Với tại s CB= K/2 lamda k thầy?
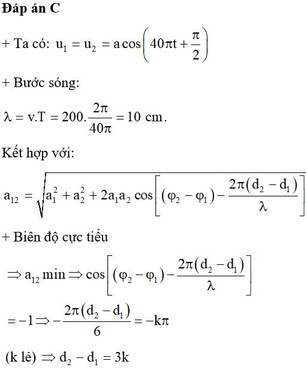





Đáp án C