Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()

Đáp án B
Gọi A là biến cố xảy ra trường hợp để yêu cầu.Không gian mẫu
![]()
Xét các trường hợp có thể xảy ra biến cố A là.
+) 2 nam Toán, 2 nữ Lý: C 8 2 . C 7 2 = 588
+) 2 nữ Toán, 2 nam Lý: C 7 2 . C 5 2 = 210
+) 1 nam Toán, 1 nam Lý, 1 nữ Toán, 1 nữ Lý
C 7 1 . C 5 1 . C 7 1 . C 8 1 = 1960
Số cách chọn cần tìm
![]()
Xác suất cần tìm là. 197 495

Đáp án B
Ta có: chọn ra 4 thầy cô từ 16 thầy cô có ![]() (cách chọn)
(cách chọn)
+ Để chọn được 4 giáo viên phải có cô giáo và đủ ba bộ môn, vậy có các trường hợp sau:
* Trường hợp 1: chọn 2 thầy toán, 1 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 2: chọn 1 thầy toán, 2 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 3: chọn 1 thầy toán, 1 cô lý, 2 cô hóa có ![]() (cách chọn)
(cách chọn)
Vậy xác suất để chọn được 4 người phải có cô giáo và có đủ ba bộ môn là
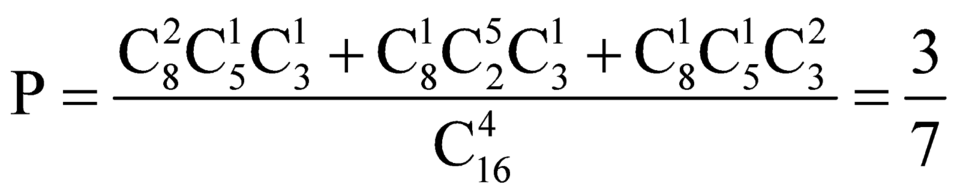

Xếp cố định 5 giáo viên Toán trên hàng, có 5! cách xếp. Có tất cả 6 khoảng trống gồm khoảng trống giữa 2 giáo viên Toán và vị trí đầu hàng, cuối hàng.
Xếp 4 giáo viên còn lại vào các khoảng trống sao cho mỗi khoảng trống chỉ chứa 1 giáo viên. Số cách xếp 4 giáo viên này là ![]() .
.
Vậy số cách xếp cần tìm là: ![]()
Chọn A.

Đáp án A
Số cách chọn ngẫu nhiên 2 giáo viên từ 30 giáo viên là:![]()
Số cách chọn ngẫu nhiên 2 giáo viên khác trường là: ![]()
Xác suất chọn 2 giáo viên khác trường là:
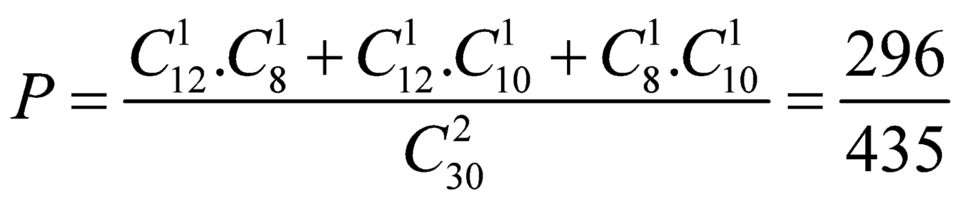

Chọn C
Xét phép thử T: “Chọn 7 cuốn sách từ 15 cuốn sách”.
Số phần tử của không gian mẫu trong phép thử là C 15 7 .
Gọi A biến cố chọn 7 cuốn sách có đủ 3 môn trong phép thử T.
Xác suất của biến cố cần tìm bằng xác suất của biến cố A.
Ta có ![]()
Vậy
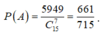

Chọn C
Gọi biến cố A: “2 giáo viên tập huấn gồm 1 thầy giáo và 1 cô giáo”.
Suy ra ![]() .
.
Vậy 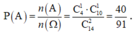 .
.
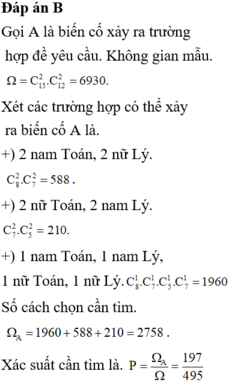
Gọi A là biến cố “Giáo viên môn Toán tham khảo bộ sách giáo khoa A”; B là biến cố “Giáo viên môn Toán tham khảo bộ sách giáo khoa B”; E là biến cố “Giáo viên môn Toán không tham khảo cả hai bộ sách giáo khoa A và B”.
Khi đó \(\overline E \) là biến cố “Giáo viên môn Toán tham khảo bộ sách giáo khoa A hoặc B”.
Ta có \(\overline E = A \cup B.\)
\(\begin{array}{l}P\left( {\overline E } \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = 63\% + 56\% - 28,5\% = 90,5\% \\ \Rightarrow P\left( E \right) = 1 - P\left( {\overline E } \right) = 1 - 90,5\% = 9,5\% \end{array}\)
Vậy tỉ lệ giáo viên môn Toán các trường trung học phổ thông của tỉnh đó không tham khảo cả hai bộ sách giáo khoa A và B là 9,5%.