VT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Vào giữa thế kỉ XIX, hoàn cảnh của Nhật Bản và các nước châu Á có những điểm tương đồng như thế nào?
0
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
\(pH = - \log \left[ {{H^ + }} \right] = - \log {8.10^{ - 8}} \approx 7,1\)
=> Độ pH không phù hợp cho tôm sú phát triển.
J
0
PT
1
CM
25 tháng 1 2018
+ Vẽ đồ thị hàm số y = cos x.
+ Vẽ đường thẳng 
+ Xác định hoành độ các giao điểm.
Ta thấy đường thẳng 
cắt đồ thị hàm số y = cos x tại các điểm có hoành độ
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
Đồ thị của hàm số \(y=sin\left(x\right)\) trên đoạn \(\left[-\pi;\pi\right]\) là:
Ta thấy đồ thị hàm số giao với đường thẳng d: \(y=\dfrac{1}{2}\) tại 2 điểm.
Do đó, phương trình \(sin\left(x\right)=\dfrac{1}{2}\) có hai giá trị \(x\in\left[-\pi;\pi\right]\) thỏa mãn
25 tháng 7 2023
Mặt nước, nắp bể và đáy bể đôi một song với nhau song song với nhau, thanh gỗ đóng vai trò là cắt tuyến cắt các mặt phẳng đáy bể tại đầu thứ nhất của thanh gỗ, cắt mặt nước giao điểm giữa phần ngâm nước và phần chưa ngâm nước của thanh gỗ, cắt nắp bể tại đầu còn lại của thanh gỗ.
Áp dụng định lí Ta lét, ta sẽ có:
tỉ lệ giữa độ dài của phân thanh gỗ bị ngâm trong nước và độ dài của cả thanh gỗ bằng tỉ lệ giữa mực nước và chiều cao của bể.
SG
1
LT
1 tháng 4 2017
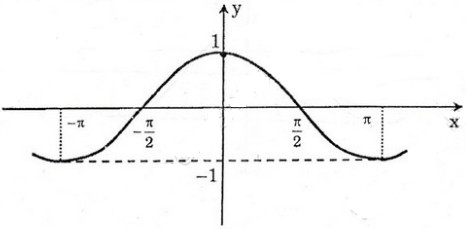
Dựa vào đồ thị hàm số y = cosx, để làm số nhận giá trị âm thì:
SG
1
LT
1 tháng 4 2017
Nhìn đồ thị y = sinx ta thấy trong đoạn [-π ; π] các điểm nằm phía trên trục hoành của đồ thị y = sinx là các điểm có hoành độ thuộc khoảng (0 ; π). Từ đố, tất cả các khoảng giá trị của x để hàm số đó nhận giá trị dương là (0 + k2π ; π + k2π) hay (k2π ; π + k2π) trong đó k là một số nguyên tùy ý.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Một đứa trẻ phát triển bình thường có chiều cao năm 3 tuổi là:
\({x_3} = 75 + 5\left( {3 - 1} \right) = 85\,\,\left( {cm} \right)\)
b) Dãy số \(\left( {{x_n}} \right)\) có là cấp số cộng
Trung bình một năm, chiều cao mỗi đứa trẻ phát triển bình thường tăng lên chính là công sai của cấp số cộng. Ta có:
\({x_n} = 75 + 5\left( {n - 1} \right) \Rightarrow \left\{ \begin{array}{l}{u_1} = 75\\d = 5\end{array} \right.\)
Vậy trung bình một năm, chiêu cao mỗi đứa trẻ phát triển bình thường tăng lên 5cm.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Từ Hình 1.20, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, - \frac{{5\pi }}{6}\)
b) Vì hàm số \(\cos x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi - \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)