Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(I=\int\dfrac{x}{1-cos2x}dx=\int\dfrac{x}{2sin^2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=\dfrac{x}{2}\\dv=\dfrac{1}{sin^2x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{2}\\v=-cotx\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int cotxdx=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int\dfrac{cosx.dx}{sinx}\)
\(=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int\dfrac{d\left(sinx\right)}{sinx}=\dfrac{-x.cotx}{2}+\dfrac{1}{2}ln\left|sinx\right|+C\)
2/ Câu 2 bữa trước làm rồi, bạn coi lại nhé
3/ \(I=\int\left(2x+1\right)ln^2xdx\)
Đặt \(\left\{{}\begin{matrix}u=ln^2x\\dv=\left(2x+1\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{2lnx}{x}dx\\v=x^2+x\end{matrix}\right.\)
\(\Rightarrow I=\left(x^2+x\right)ln^2x-\int\left(2x+2\right)lnxdx=\left(x^2+x\right)ln^2x-I_1\)
\(I_1=\int\left(2x+2\right)lnx.dx\) \(\Rightarrow\left\{{}\begin{matrix}u=lnx\\dv=\left(2x+2\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=x^2+2x\end{matrix}\right.\)
\(\Rightarrow I_1=\left(x^2+2x\right)lnx-\int\left(x+2\right)dx=\left(x^2+2x\right)ln-\dfrac{x^2}{2}+2x+C\)
\(\Rightarrow I=\left(x^2+x\right)ln^2x-\left(x^2+2x\right)lnx+\dfrac{x^2}{2}-2x+C\)
4/ \(I=\int\left(2x-1\right)cosx.dx\) \(\Rightarrow\left\{{}\begin{matrix}u=2x-1\\dv=cosx.dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=sinx\end{matrix}\right.\)
\(\Rightarrow I=\left(2x-1\right)sinx-2\int sinx.dx=\left(2x-1\right)sinx+2cosx+C\)
5/ \(I=\int\left(x^2+x+1\right)e^xdx\) \(\Rightarrow\left\{{}\begin{matrix}u=x^2+x+1\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\left(2x+1\right)dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=\left(x^2+x+1\right)e^x-\int\left(2x+1\right)e^xdx\)
\(I_1=\int\left(2x+1\right)e^xdx\) \(\Rightarrow\left\{{}\begin{matrix}u=2x+1\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I_1=\left(2x+1\right)e^x-2\int e^xdx=\left(2x+1\right)e^x-2e^x+C=\left(2x-1\right)e^x+C\)
\(\Rightarrow I=\left(x^2+x+1\right)e^x-\left(2x-1\right)e^x+C=\left(x^2-x+2\right)e^x+C\)
6/ \(I=\int\left(2x+1\right).ln\left(x+2\right)dx\)
\(\Rightarrow\left\{{}\begin{matrix}u=ln\left(x+2\right)\\dv=\left(2x+1\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x+2}\\v=x^2+x\end{matrix}\right.\)
\(\Rightarrow I=\left(x^2+x\right)ln\left(x+2\right)-\int\dfrac{x^2+x}{x+2}dx\)
\(=\left(x^2+x\right)ln\left(x+2\right)-\int\left(x-1+\dfrac{2}{x+2}\right)dx\)
\(I=\left(x^2+x\right)ln\left(x+2\right)-\dfrac{x^2}{2}+x-2ln\left|x+2\right|+C\)
Nhớ quy tắc ưu tiên khi tính nguyên hàm từng phần:
- Đặt u sẽ ưu tiên các hàm ln, log đầu tiên (luôn luôn đặt các hàm này là u nếu có mặt), sau đó đến các hàm đa thức P(x), sau đó là lượng giác hoặc e^
- Đặt dv thì theo thứ tự ngược lại, ưu tiên đặt lượng giác (sin, cos) và e^

a) Để ý đến công thức đổi cơ số logarit \(\log_2\left(1-3x\right)=\frac{1}{\ln2}\ln\left(1-3x\right)\)
Ta viết nguyên hàm đã cho dưới dạng \(I_1=\frac{1}{\ln2}\int\ln\left(1-3x\right)dx\)
Đặt \(u=\ln\left(1-3x\right)\) , \(dv=dx\)
Khi đó \(du=\frac{-3}{1-3x}dx\), \(v=x\)
Do đó :
\(I_1=\frac{1}{\ln2}\left[x\ln\left(1-3x\right)+3\int\frac{x}{1-3x}dx\right]\)
\(=\frac{1}{\ln2}\left[x\ln\left(1-3x\right)+3\int\frac{1}{3}\left(-1+\frac{1}{1-3x}\right)dx\right]\)
\(=\frac{1}{\ln2}\left[x\ln\left(1-3x\right)-\int dx+\frac{dx}{1-3x}\right]\)
\(=\frac{1}{\ln2}\left[\left(x-\frac{1}{3}\right)\ln\left(1-3x\right)-x\right]+C\)
b) Đặt \(u=\left(\ln x\right)^2\) , \(dv=\left(2x-3\right)dx\)
Khi đó \(du=2\ln x\frac{dx}{x}\) , \(v=x^2-3x\)
Do đó
\(I_2=\left(x^2-3x\right)\left(\ln x\right)^2-2\int\left(x-3\right)\ln xdx\)
\(\int\left(x-3\right)\ln xdx=I_2\)
Ta tính \(I_2\) Ta tìm nguyên hàm bằng cách lấy nguyên hàm từng phàn một làn nữa và thu được.
\(I_2=\left(\frac{1}{2}x^2-3x\right)\ln x-\int\left(\frac{1}{2}x-3\right)dx=\frac{1}{2}\left(x^2-6x\right)\ln x-\frac{1}{4}x^2+3x\)
Từ đó suy ra \(I_2=\left(x^2-3x\right)\left(\ln x\right)^2-\left(x^2-6x\right)\ln x+\frac{1}{2}x^2-6x+C\)
c) Đặt \(u=\ln x\) , \(dv=\left(4x^2+6x-7\right)dx\)
khi đó \(du=\frac{dx}{x}\) , \(v=\int\left(4x^2+6x-7\right)dx=x^4+3x^2-7x\)
Do đó
\(I_3=\left(x^4+3x^2-7x\right)\ln x-\int\frac{x^4+3x^2-7x}{x}dx\)
\(=\left(x^4+3x^2-7x\right)\ln x-\left(\frac{x^4}{4}+\frac{3x^2}{2}-7x\right)+C\)

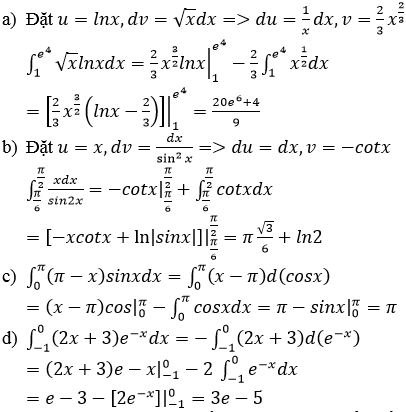
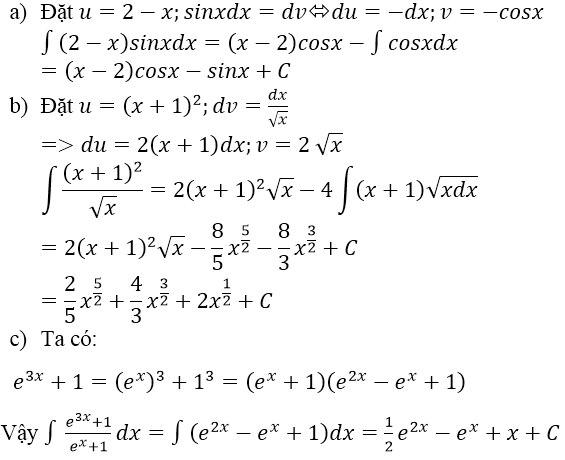

a) Áp dụng phương pháp tìm nguyên hàm từng phần:
Đặt u= ln(1+x)
dv= xdx
=>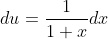 ,
, 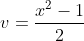
Ta có: ∫xln(1+x)dx =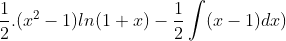
=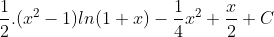
b) Cách 1: Tìm nguyên hàm từng phần hai lần:
Đặt u= (x2+2x -1) và dv=exdx
Suy ra du = (2x+2)dx, v = ex
. Khi đó:
∫(x2+2x - 1)exdx = (x2+2x - 1)exdx - ∫(2x+2)exdx
Đặt : u=2x+2; dv=exdx
=> du = 2dx ;v=ex
Khi đó:∫(2x+2)exdx = (2x+2)ex - 2∫exdx = ex(2x+2) – 2ex+C
Vậy
∫(x2+2x+1)exdx = ex(x2-1) + C
Cách 2: HD: Ta tìm ∫(x2-1)exdx. Đặt u = x2-1 và dv=exdx.
Đáp số : ex(x2-1) + C
c) Đáp số: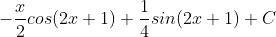
HD: Đặt u=x ; dv = sin(2x+1)dx
d) Đáp số : (1-x)sinx - cosx +C.
HD: Đặt u = 1 - x ;dv = cosxdx