Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


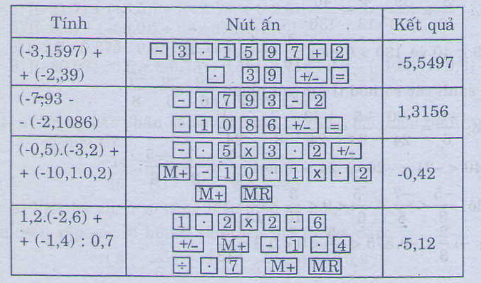
a) (−3,1597)+(−2,39)= -5,5497
b) (−0,793)−(−2,1068)= 1.3138
c) (−0,5).(−3,2)+(−10,1).0,2= -0,42
d) 1,2.(−2,6)+(−1,4):0,7=-5,12

a,\(\left(-\dfrac{5}{6}\right)^6.\left(\dfrac{6}{5}\right)^8=\left[\left(-\dfrac{5}{6}\right)^6.\left(\dfrac{6}{5}\right)^6\right].\left(\dfrac{6}{5}\right)^2=\dfrac{36}{25}\)
b,\(\left(-\dfrac{13}{8}\right)^3.\left(-\dfrac{23}{13}\right)^4=\left[\left(-\dfrac{13}{8}\right)^3.\left(-\dfrac{23}{13}\right)^3\right].\left(-\dfrac{23}{13}\right)=\left(\dfrac{23}{8}\right)^3.\left(-\dfrac{23}{13}\right)\)
c,\(\left(0,2\right)^7.5^{10}=\left(0,2.5\right)^7.5^3=125\)
d,\(\left(-0,1\right)^7.\left(-10\right)^{13}=\left(-0,1.\left(-10\right)\right)^7.\left(-10\right)^6=1000000\)

\(\left(\dfrac{\left(6,2:0,31-\dfrac{5}{6}.0,9\right).\left(0,2+0,15\right):0,2}{\left(2+1\dfrac{4}{11}.0,22:0,1\right).\dfrac{1}{33}}\right)\)
\(=\dfrac{\left(20-0,75\right).0,35:0,2}{\left(2+3\right).\dfrac{1}{33}}\)
\(=\dfrac{19,25.0,35:0,2}{5.\dfrac{1}{33}}\)
\(=\dfrac{33,6875}{\dfrac{5}{33}}=\dfrac{1617}{80}=20,2125\)
( KT lại nha ! có thể mk tính chưa đúng )
cám ơn bn nhìu vì đã giúp mk 2 câu hỏi mk đang cần gấp(đây là câu 2)![]()

a) \(VT=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)=2^{32}-1=VP\)
Vậy \(\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)=2^{32}-1\)

F=|x-1|+|x-2|+|x-3|+...+|x-100|=|x-1|+|2-x|+|x-3|+...+|100-x|
Áp dụng bđt |a|+|b|\(\ge\)|a+b|, ta có:
F=|x-1|+|2-x|+|x-3|+...+|100-x| \(\ge\) |x-1+2-x+x-3+...+100-x| = |50| = 50
=> F\(\ge\)50 => \(Min_F=50\)
P/s: mấy thánh toán đi ngang cho mik hỏi giải vậy có đúng hog?
\(F=\left|x-1\right|+\left|x-2\right|+....+\left|x-99\right|+\left|x-100\right|\)
\(F=\left(\left|x-1\right|+\left|x-100\right|\right)+\left(\left|x-2\right|+\left|x-99\right|\right)+.....+\left(\left|x-50\right|+\left|x-51\right|\right)\)
\(F=\left(\left|x-1\right|+\left|100-x\right|\right)+\left(\left|x-2\right|+\left|99-x\right|\right)+....+\left(\left|x-50\right|+\left|51-x\right|\right)\)
(do \(\left|-A\left(x\right)\right|=\left|A\left(x\right)\right|\))
Với mọi giá trị của \(x\in R\) ta có:
\(\left|x-1\right|\ge1;\left|x-2\right|\ge x-2;.....;\left|99-x\right|\ge99-x;\left|100-x\right|\ge100-x\)
\(\Rightarrow\left|x-1\right|+\left|100-x\right|\ge x-1+100-x\ge99\)
\(\left|x-2\right|+\left|99-x\right|\ge x-2+99-x\ge97\).............
\(\left|x-50\right|+\left|51-x\right|\ge x-50+51-x\ge1\)
\(\Rightarrow\left(\left|x-1\right|+\left|100-x\right|\right)+\left(\left|x-2\right|+\left|99-x\right|\right)+....+\left(\left|x-50\right|+\left|51-x\right|\right)\ge99+97+.....+3+1\)
\(\Rightarrow\left(\left|x-1\right|+\left|100-x\right|\right)+\left(\left|x-2\right|+\left|99-x\right|\right)+....+\left(\left|x-50\right|+\left|51-x\right|\right)\ge\dfrac{\left(99+1\right).50}{2}\)
\(\Rightarrow\left(\left|x-1\right|+\left|100-x\right|\right)+\left(\left|x-2\right|+\left|99-x\right|\right)+....+\left(\left|x-50\right|+\left|51-x\right|\right)\ge2500\)
Dấu "=" sảy ra khi:
\(\left\{{}\begin{matrix}x-50\ge0\\51-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge50\\x\le51\end{matrix}\right.\Rightarrow50\le x\le51\)
Vậy GTNN của biểu thức F là 2500 đạt được khi và chỉ khi \(50\le x\le51\)
Mình cũng không chắc đâu! Chúc bạn học tốt!!!

a: \(\dfrac{x+1}{5}+\dfrac{x+1}{6}=\dfrac{x+1}{7}+\dfrac{x+1}{8}\)
\(\Leftrightarrow\left(x+1\right)\left(\dfrac{1}{5}+\dfrac{1}{6}-\dfrac{1}{7}-\dfrac{1}{8}\right)=0\)
=>x+1=0
hay x=-1
b: \(\Leftrightarrow\left(\dfrac{x-1}{2009}-1\right)+\left(\dfrac{x-2}{2008}-1\right)=\left(\dfrac{x-3}{2007}-1\right)+\left(\dfrac{x-4}{2006}-1\right)\)
=>x-2010=0
hay x=2010
c: \(\Leftrightarrow\dfrac{1}{x+2}-\dfrac{1}{x+5}+\dfrac{1}{x+5}-\dfrac{1}{x+10}+\dfrac{1}{x+10}-\dfrac{1}{x+17}=\dfrac{x}{\left(x+2\right)\left(x+17\right)}\)
\(\Leftrightarrow\dfrac{x}{\left(x+2\right)\left(x+17\right)}=\dfrac{x+17-x-2}{\left(x+2\right)\left(x+17\right)}\)
=>x=15

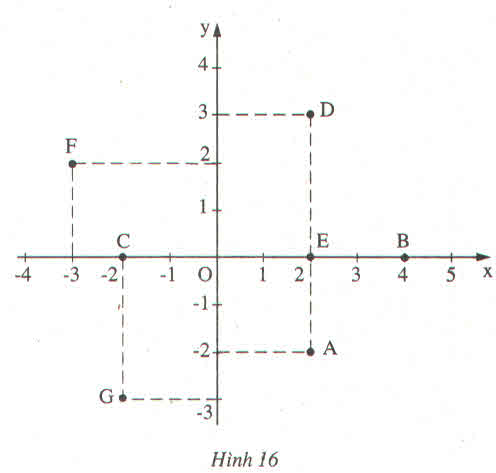
a) Tọa độ các điểm trong hình vẽ là:
A(2;-2); B(4;0); C(-2;0); D(2;3); E(2;0);F(-3;2); G(-2;-3)
b) Ta có hình vẽ ∆ABC:
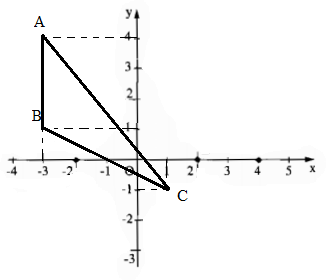
A(-3;4); B(-3;1); C(1;-1).

\(\text{a) }\dfrac{\left(-6\right)^6}{216}=\dfrac{6^6}{216}=\dfrac{6^6}{6^3}=6^3=216\)
\(\text{b) }\dfrac{64}{\left(-4\right)^5}=-\dfrac{64}{4^5}=-\dfrac{4^3}{4^5}=-\dfrac{1}{4^2}=-\dfrac{1}{16}\)
\(\text{c) }\dfrac{900}{\left(-30\right)^3}=-\dfrac{900}{30^3}=-\dfrac{30^2}{30^3}=-\dfrac{1}{30}\)
\(\text{d) }\dfrac{225}{15^3}=\dfrac{15^2}{15^3}=\dfrac{1}{15}\)

a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)