Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
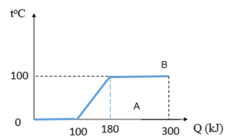
Nhìn vào đồ thị ta có thể biết được nhiệt lượng của nước đá thu vào ở 0 0 C . để nó nóng chảy hoàn toàn là 100KJ

Khi được làm lạnh tới 00C, nước toả ra một nhiệt lượng bằng: Q1 = m1.C1(t – 0) = 0,5.4200.20 = 42 000JĐể làm “nóng” nước đá tới 00C cần tốn một nhiệt lượng:Q2 = m2.C2(0 – t2) = 0,5.2100.15 = 15 750JBây giờ muốn làm cho toàn bộ nước đá ở 00C tan thành nước cũng ở 00C cần một nhiệt lượng là: Q3 = λ.m2 = 3,4.105.0,5 = 170 000JNhận xét:+ Q1 > Q2 : Nước đá có thể nóng tới 00C bằng cách nhận nhiệt lượng do nước toả ra+ Q1 – Q2 < Q3 : Nước đá không thể tan hoàn toàn mà chỉ tan một phần.Vậy sau khi cân bằng nhiệt được thiết lập nước đá không tan hoàn toàn và nhiệt độ của hỗn hợp là 00C

Đáp án: B
- Dựa vào đồ thị ta thấy. Ban đầu cần cung cấp 100kJ để nước đá tan hoàn toàn, lúc này nhiệt độ nước vẫn là 0 0 C . Đến khi nhiệt lượng cung cấp là 180kJ nữa thì nước bắt đầu sôi.
- Vậy để đun nước từ 0 0 C lên đến 100 0 C thì cần 80kJ

200g=0,2kg
50g=0,05kg
100g=0,1kg
ta có phương trình cân bằng nhiệt:
Qtỏa=Qthu
\(\Leftrightarrow Q=m_1C_1\left(0--10\right)+m_1\lambda+m_1C_2\left(100-0\right)+m_1L\)
\(\Leftrightarrow Q=3600+68000+84000+460000\)
\(\Leftrightarrow Q=615600J\)
nếu bỏ cục nước đá vào nước thì phương trình cân bằng nhiệt là:
Qtỏa=Qthu
\(\Leftrightarrow Q_n+Q_{nh}=Q_{nđ}\)
\(\Leftrightarrow Q_2+Q_3=Q_1\)
\(\Leftrightarrow m_2C_2\left(t_2-t\right)+m_3C_3\left(t_3-t\right)=m_1C_1\left(t-t_1\right)+\left(m_1-0,05\right)\lambda\)
\(\Leftrightarrow4200m_2\left(20-0\right)+88\left(20-0\right)=360\left(0--10\right)+3,4.10^5\left(0,2-0,05\right)\)
\(\Leftrightarrow84000m_2+1760=54600\)
\(\Rightarrow m_2=0,63kg\)
chú ý ở câu b:
nhiệt độ cân bằng là 0 vì nước đá chưa tan hết.
khối lượng nhân cho lamđa phải trừ đi cho phần chưa tan hết
chúc bạn thành công nhé![]()

Gọi nhiệt lượng của nước là \(Q_t\) từ \(20^oC\) về \(0^oC\) và của nước đá tan hết là \(Q_{thu}\), ta có:
\(Q_t=m_2c_2.\left(20-0\right)=0,3.4200.20=25200J\)
\(Q_{thu}=m_1.\lambda=0,1.3,4.10^5=34000J\)
Ta thấy Qthu > Qtỏa nên nước đá không tan hết. Lượng nước đá chưa tan hết là:
\(m=\frac{Q_{thu}-Q_{tỏa}}{\lambda}\)\(=\frac{8800}{3,4.10^5}=0,026\left(kg\right)\)

Câu 1:
a) Trọng lực tác dụng lên vật:
\(P=\dfrac{A}{h}=\dfrac{600}{20}=30N\)
b) P = 10m => \(m=\dfrac{P}{10}=\dfrac{30}{10}=3kg\)
Thế năng tại độ cao 5m:
Wt = 10mh' = 10.3.5 = 150J
Theo đl bảo toàn cơ năng nên: Wt + Wd = W = 600J
Động năng tại độ cao 5m:
Wd = W - Wt = 600 - 150 = 450J
Câu 2:
Tóm tắt:
t1 =200C
t2 = 1000C
t = 550C
m2 = 10lit = 10kg
m1 = ?
Giải:
Áp dụng PT cân bằng nhiệt:
Q1 = Q2
=> m1c1(t - t1) = m2c2(t2 - t)
<=> m1( t - t1) = m2(t2 - t)
<=> m1 (55 - 20) = 10.(100 - 55)
<=> 35m1 = 450
=> m1 = 12,8l
Câu 5:
Không, vì một phần nhiệt năng của củi khô bị đốt cháy được truyền cho ấm và không khí xung quanh. Tổng phần nhiệt năng mà nước nhận đuợc và nhiệt năng truyền cho ấm, không khí xung quanh vẫn bằng năng lượng do củi khô bị đốt cháy tỏa ra. Nghĩa là, năng lượng vẫn được bảo toàn
Câu 3:
Đổi 18kW = 18000W ; 54km/h = 15m/s
a) Lực mà động cơ sinh ra:
\(P=F.v\Rightarrow F=\dfrac{P}{v}=\dfrac{18000}{15}=1200N\)
Công cơ học mà động cơ sinh ra:
\(A=F.s=1200.100000=120000000J\)
b) Nhiệt lượng tỏa ra:
Qtoa = mq = 10.46.106 = 460000000J
Hiệu suất của động cơ:
\(H=\dfrac{A}{Q}=\dfrac{120000000}{460000000}.100\%=26,08\%\)
Câu 4:
Tóm tắt:
c1 = 460J/Kg.K
m1 = 200g = 0,2kg
m2 = 690g = 0,69kg
t2 = 200C
c2 = 4200J/kg.K
t = 220C
Q2 = ?
t1 = ?
Giải:
a) Nhiệt lượng do nước thu vào:
Q2 = m2c2( t - t2) = 0,69.4200.(22 - 20) = 5796J
b) Nhiệt độ ban đầu của kim loại
Áp dụng PT cân bằng nhiệt:
Q1 = Q2
<=> m1c1( t1 - t) = Q2
<=> 0,2.460(t1 - 22) = 5796
<=> \(t_1=\dfrac{5796}{0,2.460}+22=85^0C\)

a)ta có:
nhiệt lượng nước đá cần để tan hết là:
\(Q_1=m_1C_1\left(t-t_1\right)+m_1\lambda\)
\(\Leftrightarrow Q_1=33600+537600=571200J\)
nhiệt lượng nước tỏa ra là:
\(Q_2=m_2C_2\left(t_2-t\right)=537600J\)
nhiệt lượng bình tỏa ra là:
\(Q_3=m_3C_3\left(t_3-t\right)=6080J\)
do Q1>(Q2+Q3) nên nước đá chưa tan hết
b)do nước đá chưa tan hết nên nhiệt độ cuối cùng của bình nhiệt lượng kế là 0 độ C

Đáp án: D
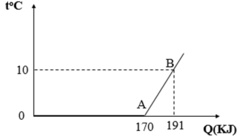
- Nhìn vào đồ thị ta có thể biết được nhiệt lượng của nước đá thu vào ở 0 0 C để nó nóng chảy hoàn toàn là 170kJ.
Q t h u = m . λ = Q t h u : λ
- Khối lượng của khối nước đá là:
m = 170000 : 340000 = 0,5 (kg)