K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 7 2021
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
OP
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2022
Đặt \(\left\{{}\begin{matrix}\sqrt{2x^2+5x+12}=a>0\\\sqrt{2x^2+3x+2}=b>0\end{matrix}\right.\) \(\Rightarrow x+5=\dfrac{a^2-b^2}{2}\)
Phương trình trở thành:
\(a+b=\dfrac{a^2-b^2}{2}\)
\(\Leftrightarrow\left(a-b-2\right)\left(a+b\right)=0\)
\(\Leftrightarrow a-b-2=0\) (do \(a+b>0\))
\(\Leftrightarrow a=b+2\)
\(\Leftrightarrow\sqrt{2x^2+5x+12}=\sqrt{2x^2+3x+2}+2\)
\(\Leftrightarrow2x^2+5x+12=2x^2+3x+6+4\sqrt{2x^2+3x+2}\)
\(\Leftrightarrow x+3=2\sqrt{2x^2+3x+2}\) (\(x\ge-3\))
\(\Leftrightarrow x^2+6x+9=4\left(2x^2+3x+2\right)\)
\(\Leftrightarrow7x^2+6x-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{1}{7}\end{matrix}\right.\)
Y
26 tháng 6 2023
\(a,\dfrac{3}{\sqrt{12x-1}}\) xác định \(\Leftrightarrow12x-1>0\Leftrightarrow12x>1\Leftrightarrow x>\dfrac{1}{12}\)
\(b,\sqrt{\left(3x+2\right)\left(x-1\right)}\) xác định \(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}3x+2\ge0\\x-1\ge0\end{matrix}\right.\\\left[{}\begin{matrix}3x+2\le0\\x-1\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x\ge-\dfrac{2}{3}\\x\ge1\end{matrix}\right.\\\left[{}\begin{matrix}x\le-\dfrac{2}{3}\\x\le1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-\dfrac{2}{3}\\x\ge1\end{matrix}\right.\)
\(c,\sqrt{3x-2}.\sqrt{x-1}\) xác định \(\Leftrightarrow\left[{}\begin{matrix}3x-2\ge0\\x-1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{2}{3}\\x\ge1\end{matrix}\right.\) \(\Leftrightarrow x\ge1\)
\(d,\sqrt{\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}}\) xác định \(\Leftrightarrow-x+5>0\Leftrightarrow x< 5\)
10 tháng 8 2023
1: ĐKXĐ: -2/2x-2>=0
=>2x-2<0
=>x<1
2: ĐKXĐ: 2/3x-1>=0
=>3x-1>0
=>x>1/3
3: ĐKXĐ: 2x-2/(-2)>=0
=>2x-2<=0
=>x<=1
4: ĐKXĐ: (3x-2)/5>=0
=>3x-2>=0
=>x>=2/3
5: ĐKXĐ: (x-2)/(x+3)>=0
=>x>=2 hoặc x<-3
23 tháng 3 2021
a) ĐKXĐ: \(x\notin\left\{\dfrac{1}{3};-\dfrac{1}{3}\right\}\)
Ta có: \(\dfrac{12}{1-9x^2}=\dfrac{1-3x}{1+3x}-\dfrac{1+3x}{1-3x}\)
\(\Leftrightarrow\dfrac{\left(1-3x\right)^2}{\left(1+3x\right)\left(1-3x\right)}-\dfrac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}=\dfrac{12}{\left(1-3x\right)\left(1+3x\right)}\)
Suy ra: \(9x^2-6x+1-9x^2-6x-1=12\)
\(\Leftrightarrow-12x=12\)
hay x=-1(thỏa ĐK)
Vậy: S={-1}
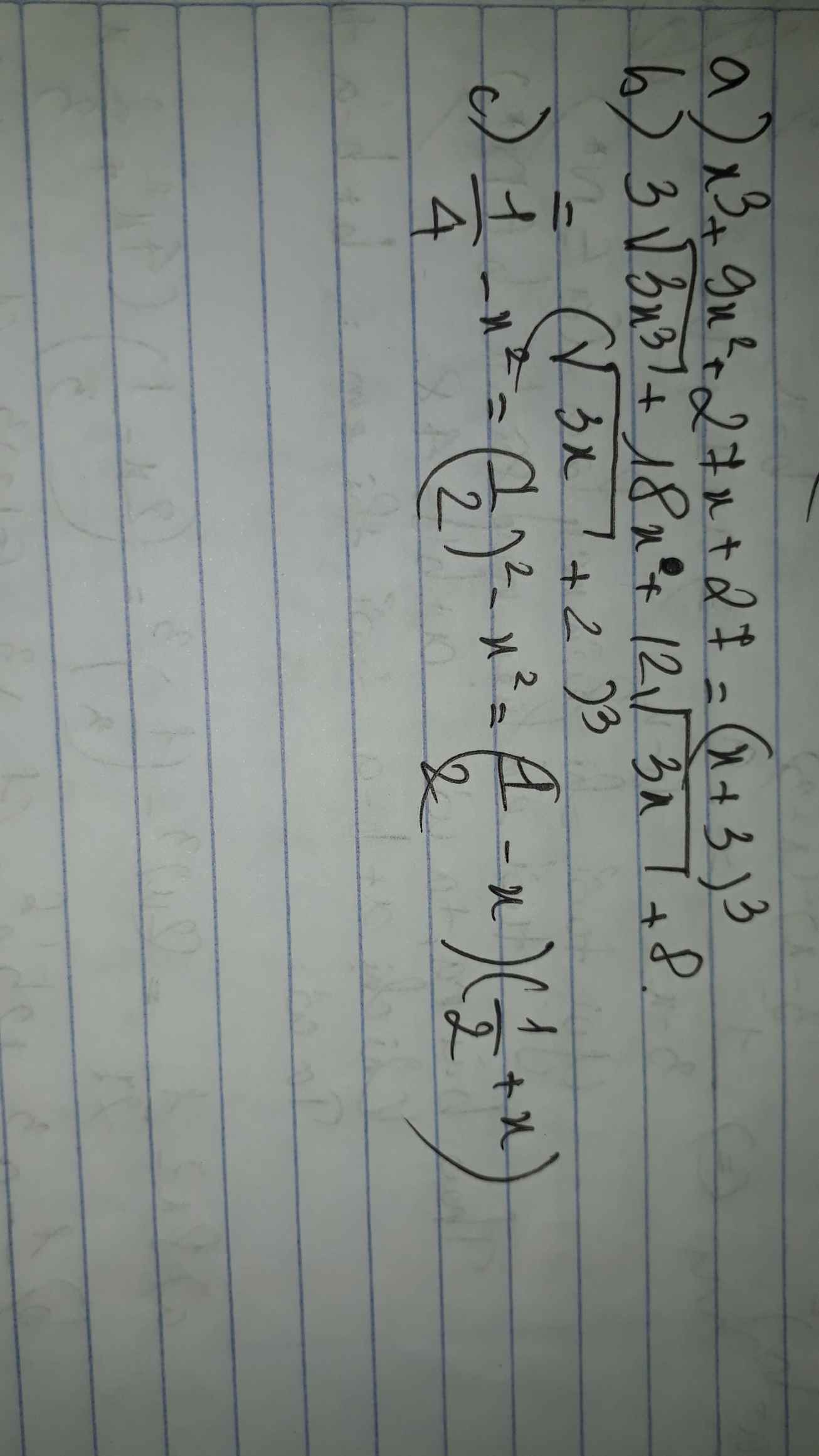
bằng phuiong pháp đặt ẩn phụ hoàn toàn nha
Đặt \(x^2+3x=t\left(t>0\right)\)
Ta có: \(\sqrt{x^2+3x+12}=x^2+3x\)
\(\Rightarrow\sqrt{t+12}=t\)
\(\Rightarrow t+12=t^2\)
\(\Rightarrow t^2-t-12=0\)
\(\Rightarrow t\left(t-4\right)+3\left(t-4\right)=0\)
\(\Rightarrow\left(t-4\right)\left(t+3\right)=0\Rightarrow\orbr{\begin{cases}t=4\left(t/m\right)\\t=-3\left(loai\right)\end{cases}}\)
Ta có: \(x^2+3x=4\)
\(\Rightarrow x^2+3x-4=0\)
\(\Rightarrow x\left(x+4\right)-\left(x+4\right)=0\)
\(\Rightarrow\left(x+4\right)\left(x-1\right)=0\Rightarrow\orbr{\begin{cases}x=-4\\x=1\end{cases}}\)
Chúc bạn học tốt.