Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta biễu diễn vị trí của M và N trên đường tròn.

Từ hình vẽ, ta thấy rằng có hai khả năng xảy ra của độ lệch pha


Đáp án A
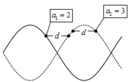
+ Khi có sóng dừng, phần tử dây cách nút một đoạn d dao dộng với biên độ a = A sin 2 π d λ , phần tử dây cách bụng một đoạn d dao động với biên độ a = A cos 2 π d λ .
+ Với a 2 = 3 mm, lớn hơn a 1 = 2 mm → hai điểm gần nhau nhất dao động cùng biên độ a 2 phải đối xứng nhau qua bụng sóng, hai điểm dao động với cùng biên độ a 1 phải đối xứng nhau qua nút sóng
→ a 1 = A sin π d 2 a 2 = A cos π d 2 ↔ 2 = A sin 10 π λ 3 = A c o s 10 π λ → A = 2 2 + 3 2 = 13 λ = 53 mm.
+ Khoảng cách giữa hai nút sóng liên tiếp là Δ d = λ 2 = 26 , 7 m m

Cứ giữa 2 bụng liên tiếp có 2 điểm dao động biên độ 2√⇒ 20 điểm thì k=10
Vậy λ=2cm

Đáp án D
Theo giả thuyết điểm N dao động nhanh pha hơn điểm M: 2 π 3 (tương ứng λ/3).
Cùng với giả thuyết hai điểm có cùng biên độ, điểm N sớm pha hơn M, vậy ta kết luận pha của hai điểm như hình vẽ.
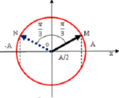
Vậy điểm M có pha π 6 , như hình vẽ. Và biểu thức liên hệ giữa biên độ là:
x = 3 2 A ⇒ A = 2 3 x = 2 3 . 3 = 2 3 c m

Đáp án C
+ Hai điểm M, N dao động vuông pha với nhau, do M gần nguồn sóng hơn nên khi N ở vị trí thấp nhất thì M đã đạt trạng thái thấp nhất trước đó t = T 4 Vậy thời gian ngắn nhất để M chuyển trạng thái như N là t ' = 3 T 4 = 3 4 f = 3 80 s

Chọn D
+Biên độ sóng tại M:
A M = 2 a cos π d 1 - d 2 λ = 2 a cos π d 1 - d 2 v f =0 cm


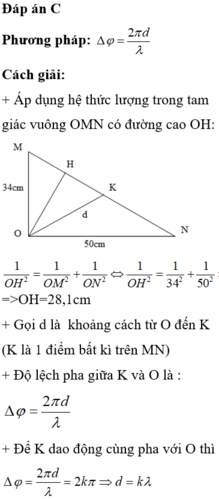


Góc MOA và NOA biểu diễn ''độ lệch pha biên độ'' của M; N với điểm bụng bụng gần nó nhât. Gọi d là khoảng cách từ 1 điểm đến điểm bụng gần nó nhất khi đó độ lệch pha biên độ được tính.
\(\Delta\)φ=\(\frac{2\pi\text{d}}{\text{λ}}\text{ }\)
Theo bài ra:
\(\begin{cases}\frac{1}{20}\left(s\right)=\frac{T}{4}\\\frac{1}{15}\left(s\right)=\frac{T}{3}\end{cases}\leftrightarrow\begin{cases}\text{∠}-MOM=\frac{2\pi}{4}=\frac{\pi}{2}\\\text{∠}-NON=\frac{2\pi}{3}\end{cases}\)
\(\rightarrow\begin{cases}MOA=\frac{\pi}{4}\\NOA=\frac{\pi}{6}\end{cases}\) \(\leftrightarrow\begin{cases}2\pi\frac{MP}{\text{λ}}=\frac{\pi}{4}\\2\pi\frac{NP}{\text{λ}}=\frac{\pi}{6}\end{cases}\) \(\leftrightarrow\begin{cases}MP=\frac{\text{λ}}{8}\\NP=\frac{\text{λ}}{12}\end{cases}\)
\(\Rightarrow\frac{\text{λ}}{8}-\frac{\text{λ}}{12}=0,2\leftrightarrow\text{λ}=4,8cm\)
2πdλ