
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án: C
6 x 2 - 9 y 2 = 54
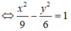
Phương trình hai đường tiệm cận của hypebol là:
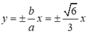

Chọn D.
Ta có: ± b a = ± 2 3 ⇒ a = 3 b = 2 .
Phương trình (H) : x 2 9 - y 2 4 = 1

Đáp án: D
Hypebol có hai đường tiệm cận
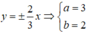
Vậy phương trình của hypebol là:
x 2 9 - y 2 4 = 1

Chọn D.
Ta có a 2 = 3 b 2 = 1 ⇒ a = 3 b = 1 :
Đường tiệm cận của (H) là y = 1 3 x và y = - 1 3 x hay x - 3 y = 0 và x + 3 y = 0 .
Gọi là góc giữa hai đường tiệm cận, ta có
cos a = 1 . 1 - 3 . 3 1 2 + - 3 2 . 1 2 + 3 2 = 1 2 ⇒ a = 60 0
Ví dụ: D = [a ; b) thì phải tính thì ta phải tìm ba giới hạn là
thì ta phải tìm ba giới hạn là
- Để tìm đường tiệm cận ngang ta phải có giới hạn của hàm số ở vô tận:
- Để tìm đường tiệm cận đứng thì hàm số phải ra vô tận khi x tiến đến một giá trị x0 : thì (Δ) : x = x0 là đường tiệm cận đứng của (C) : y = f(x).
thì (Δ) : x = x0 là đường tiệm cận đứng của (C) : y = f(x).
Nếu
- Để tìm đường tiệm cận xiên của (C) : y = f(x), trước hết ta phải có điều kiện
+ Phân tích biểu thức y = f(x) thành dạng y = f(x) = ax + b + ε(x)
(a ≠ 0) là đường tiệm cận xiên của (C) : y = f(x)
+ Hoặc ta tìm a và b bởi công thức:
Khi đó y = ax + b là phương trình đường tiệm cận xiên của (C) : y = f(x).
Ghi chú :
Đường tiệm cận của một số hàm số thông dụng :
- Hàm số có hai đường tiệm cận đứng và ngang lần lượt có phương trình
có hai đường tiệm cận đứng và ngang lần lượt có phương trình
là
- Với hàm số (không chia hết và a.p ≠ 0), ta chia đa thức để có:
(không chia hết và a.p ≠ 0), ta chia đa thức để có:
thì hàm số có hai đường tiệm cận đứng và xiên lần lượt có phương trình là:
- Hàm hữu tỉ
- Với hàm hữu tỉ, giá trị x0 làm mẫu triệt tiêu nhưng không làm tử triệt tiêu thì x = x0 chính là phương trình đường tiệm cận đứng.
- Hàm số có thể viết ở dạng
có thể viết ở dạng
hàm số sẽ có hai đường tiệm cận xiên:
 có các đường tiệm cận với phương trình là kết quả nào
có các đường tiệm cận với phương trình là kết quả nào
Ví dụ: Đồ thị hàm số
sau đây?
(A) x = 3, y = 1 ; (B) x= 3, x = -3, y = 1 ;
(C)x = -3, y = 1 ; (D) x = 3, y = 2x - 4.
Giải

là phương trình đường tiệm cận ngang.
Chon đáp án C.
Anh này là thánh chép mạng ồi