NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
0
PT
1
AS
4
15 tháng 10 2017
ta ví dụ a/b = 5/4
ta có 5/4 ... 5+1/4+1
= 5/4 ... 6/5
ta quy đồng được :5/4 = 25/20 ; 6/5 = 24/20
=> a/b > a+m/b+m
15 tháng 10 2017
Ta có : a/b = a*(b+m)/b*(b+m) = ab+am/b*(b+m)
a+m/b+m = (a+m)*b/(b+m)*b = ab+bm/b*(b+m)
Vì a/b > 1 => a > b hay am > bm
Vậy ab+am/b*(b+m) > ab+bm/b*(b+m) Hay a/b > a+m/b+m
DD
Đoàn Đức Hà
Giáo viên
16 tháng 9 2021
\(\frac{a}{b}-\frac{a+m}{b+m}=\frac{ab+am-ab-bm}{b\left(b+m\right)}=\frac{m\left(a-b\right)}{b\left(b+m\right)}\)
\(\frac{a}{b}>1\Rightarrow a>b>0\)
Nếu \(m>0\)thì \(\frac{m\left(a-b\right)}{b\left(b+m\right)}>0\Rightarrow\frac{a}{b}>\frac{a+m}{b+m}\).
Nếu \(m< 0\)thì \(\frac{m\left(a-b\right)}{b\left(b+m\right)}< 0\Rightarrow\frac{a}{b}< \frac{a+m}{b+m}\).
V
14 tháng 10 2017
Câu này lớp 7
Ta có : a/b > 1
=> a > b > 0
=> a ; b \(\in N\)
Ta có : \(\frac{a}{b}=\frac{a.\left(b+m\right)}{b\left(b+m\right)}=\frac{a.b+a.m}{b^2+b.m}\)
\(\frac{a+m}{b+m}=\frac{\left(a+m\right)b}{\left(b+m\right).b}=\frac{a.b+b.m}{b^2+b.m}\)
Vì a > b => ( a.b + a.m ) > ( a.b + b.m )
=> \(\frac{a.b+a.m}{b^2+b.m}>\frac{a.b+b.m}{b^2+b.m}\)
\(\Rightarrow\frac{a}{b}>\frac{a+m}{b+m}\)
15 tháng 10 2017
Không phải,câu này là toán nâng cao lớp 5 mà.Cô giáo mik in cho cả quyển.
CC
0
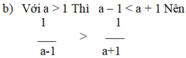
Ta có: \(b=a+1\Rightarrow b-a=1\)
\(\frac{1}{a}\times\frac{1}{b}=\frac{1}{a\times b}\)(1)
\(\frac{1}{a}-\frac{1}{b}=\frac{b-a}{a\times b}=\frac{1}{a\times b}\)(2)
Từ (1) và (2) suy ra \(\frac{1}{a}\times\frac{1}{b}=\frac{1}{a}-\frac{1}{b}\)
Ta có: b=a+1=>b-a=1
Theo bài ra ta có: \(\frac{1}{a}.\frac{1}{b}=\frac{1}{a.b}=\frac{b-a}{a.b}\left(b-a=1\right)=\frac{b}{a.b}=\frac{a}{a.b}=\frac{1}{a}-\frac{1}{b}\)
=>\(\frac{1}{a}.\frac{1}{b}=\frac{1}{a}-\frac{1}{b}\)