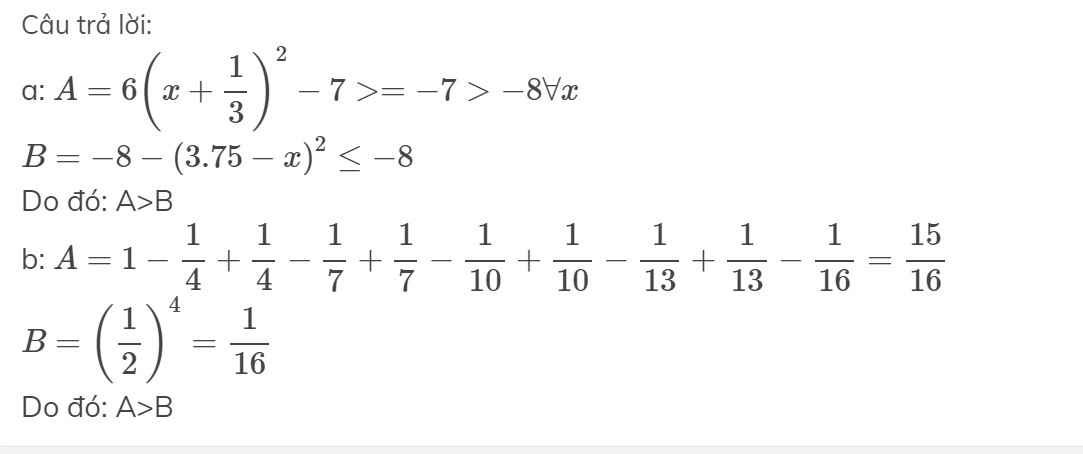Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(A=6\left(x+\dfrac{1}{3}\right)^2-7>=-7>-8\forall x\)
\(B=-8-\left(3.75-x\right)^2\le-8\)
Do đó: A>B
b: \(A=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{16}=\dfrac{15}{16}\)
\(B=\left(\dfrac{1}{2}\right)^4=\dfrac{1}{16}\)
Do đó: A>B

a) \(\left(x+\dfrac{1}{2}\right)+\left(x+\dfrac{1}{6}\right)+\left(x+\dfrac{1}{12}\right)+....+\left(x+\dfrac{1}{9900}\right)\)
\(\Leftrightarrow\left(x+x+x+...+x\right)+\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{9900}\right)=1\)
\(\Leftrightarrow50x+\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\right)=1\)
\(\Leftrightarrow50x+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)=1\)
\(\Leftrightarrow50x+\left(1-\dfrac{1}{100}\right)=1\)
\(\Leftrightarrow50x+\dfrac{99}{100}=1\)
\(\Leftrightarrow50x=\dfrac{1}{100}\Rightarrow x=\dfrac{1}{5000}\)
b) \(A=\dfrac{3^2}{1.4}+\dfrac{3^2}{4.7}+\dfrac{3^2}{7.10}+...+\dfrac{3^2}{202.205}\)
\(A=\dfrac{3^2}{3}\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{202}-\dfrac{1}{205}\right)\)
\(A=\dfrac{9}{3}\cdot\left(1-\dfrac{1}{205}\right)\)
\(A=\dfrac{9}{3}\cdot\dfrac{204}{205}=\dfrac{615}{205}\)
a) \(\left(x+\dfrac{1}{2}\right)+\left(x+\dfrac{1}{6}\right)+\left(x+\dfrac{1}{12}\right)+....+\left(x+\dfrac{1}{9900}\right)=1\)
\(\Leftrightarrow\left(x+x+x+...+x\right)+\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{9900}\right)=1\)
\(\Leftrightarrow\left(x+x+x+...+x\right)+\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\right)=1\)
Có tất cả : (99 - 1) : 1 + 1 = 99 (số x)
\(\Rightarrow99x+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)=1\)
\(\Rightarrow99x+\left(1-\dfrac{1}{100}\right)=1\)
\(\Rightarrow99x+\dfrac{99}{100}=1\Rightarrow99x=1-\dfrac{99}{100}\)
\(\Rightarrow99x=\dfrac{1}{100}\Rightarrow x=\dfrac{1}{100.99}=\dfrac{1}{9900}\)
b) \(A=\dfrac{3^2}{1.4}+\dfrac{3^2}{4.7}+\dfrac{3^2}{7.10}+....+\dfrac{3^2}{202.205}\)
\(A=\dfrac{3^2}{3}\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{202}-\dfrac{1}{205}\right)\)
\(A=\dfrac{9}{3}\cdot\left(1-\dfrac{1}{205}\right)\)
\(A=3\cdot\dfrac{204}{205}=\dfrac{615}{205}\)

a)hình như đề sai thì phải
sửa lại
\(\left(\dfrac{1}{7}-\dfrac{2}{5}\right).\dfrac{2016}{2017}+\left(\dfrac{13}{7}+\dfrac{2}{5}\right).\dfrac{2016}{2017}\)
=\(\dfrac{2016}{2017}.\left(\dfrac{1}{7}-\dfrac{2}{5}+\dfrac{13}{7}+\dfrac{2}{5}\right)\)
=\(\dfrac{2016}{2017}.2=\dfrac{4032}{2017}\)

a: \(\dfrac{x+1}{5}+\dfrac{x+1}{6}=\dfrac{x+1}{7}+\dfrac{x+1}{8}\)
\(\Leftrightarrow\left(x+1\right)\left(\dfrac{1}{5}+\dfrac{1}{6}-\dfrac{1}{7}-\dfrac{1}{8}\right)=0\)
=>x+1=0
hay x=-1
b: \(\Leftrightarrow\left(\dfrac{x-1}{2009}-1\right)+\left(\dfrac{x-2}{2008}-1\right)=\left(\dfrac{x-3}{2007}-1\right)+\left(\dfrac{x-4}{2006}-1\right)\)
=>x-2010=0
hay x=2010
c: \(\Leftrightarrow\dfrac{1}{x+2}-\dfrac{1}{x+5}+\dfrac{1}{x+5}-\dfrac{1}{x+10}+\dfrac{1}{x+10}-\dfrac{1}{x+17}=\dfrac{x}{\left(x+2\right)\left(x+17\right)}\)
\(\Leftrightarrow\dfrac{x}{\left(x+2\right)\left(x+17\right)}=\dfrac{x+17-x-2}{\left(x+2\right)\left(x+17\right)}\)
=>x=15

Từ a/b=c/d⇒a/c=b/d
Áp dụng tính chất dãy tỉ số bằng nhau
a/c=b/d=a+b/c+d
⇒a^3/c^3=b^3/d^3=(a+b)^3/(c+d)^3 (1)
Từ a^3/c^3=b^3/d^3=a^3-b^3/c^3-d^3 (2)
Từ (1) và (2)
⇒(a+b)^3/(c+d)^3=a^3-b^3/c^3-d^3

1/a/ \(\left(\dfrac{2}{5}-3x\right)^2=\dfrac{9}{25}\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{2}{5}-3x=\dfrac{3}{5}\\\dfrac{2}{5}-3x=-\dfrac{3}{5}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}3x=-\dfrac{1}{5}\\3x=1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{15}\\x=\dfrac{1}{3}\end{matrix}\right.\)
Vậy ...
b/ \(\left(\dfrac{2}{3}x-\dfrac{1}{5}\right)^5=\dfrac{1}{243}\)
\(\Leftrightarrow\dfrac{2}{3}x-\dfrac{1}{5}=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{2}{3}x=\dfrac{8}{15}\)
\(\Leftrightarrow x=\dfrac{4}{5}\)
Vậy .........
2/ a/
Ta có :
\(5^{222}=\left(5^2\right)^{111}=25^{111}\)
\(2^{555}=\left(2^5\right)^{111}=32^{111}\)
Vì \(25^{111}< 32^{111}\Leftrightarrow5^{222}< 2^{555}\)
b/ Ta có :
\(3^{48}=\left(3^4\right)^{12}=81^{12}\)
\(4^{36}=\left(4^3\right)^{12}=64^{12}\)
Vì \(81^{12}>64^{12}\Leftrightarrow3^{48}>4^{36}\)

\(\dfrac{-1}{4}x+\dfrac{2}{3}=\dfrac{5}{9}\)\(\Rightarrow\)\(\dfrac{-1}{4}x=\dfrac{5}{9}-\dfrac{2}{3}\)=\(\dfrac{-1}{9}\)
\(\Rightarrow\) x = \(\dfrac{-1}{9}:\dfrac{-1}{4}\)=\(\dfrac{4}{9}\).
\(x.\left(\dfrac{3}{5}\right)^3=\dfrac{3}{5}\)
\(\Rightarrow\)x=\(\dfrac{3}{5}:\left(\dfrac{3}{5}\right)^3=\left(\dfrac{3}{5}\right)^{-2}\)= \(2\dfrac{7}{9}\)
\(\left|x\right|\) + \(\dfrac{1}{5}=2-\left(\dfrac{2}{3}-\dfrac{3}{4}\right)\)=2 - \(\dfrac{-1}{12}\)=2\(\dfrac{1}{12}\)
\(\Rightarrow\)\(\left|x\right|\)=\(2\dfrac{1}{12}\)-\(\dfrac{1}{5}\)=\(1\dfrac{53}{60}\)
\(\Rightarrow\)x=\(\left[{}\begin{matrix}1\dfrac{53}{60}\\-1\dfrac{53}{60}\end{matrix}\right.\)
\(\left(\dfrac{-3}{4}\right)^x=\dfrac{81}{256}\)=\(\dfrac{(-3)^4}{4^4}\)=\(\left(\dfrac{-3}{4}\right)^4\)
\(\Rightarrow\) x = 4
14 Mẹo Vặt Sáng Tạo Dành Cho Học Sinh - YouTube
thử xem mẹo thứ 5 đi chứ theo mk đây là bài toán dễ lớp 6

a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)