IA
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3
LV
5
MA
7 tháng 5 2017
Ta có:
\(A=\frac{1946}{1986}=1-\frac{40}{1986}\)
\(B=\frac{1968}{2008}=1-\frac{40}{2008}\)
Vì \(\frac{40}{1986}>\frac{40}{2008}\Rightarrow1-\frac{40}{1986}< 1-\frac{40}{2008}\)
\(\frac{1946}{1986}< \frac{1968}{2008}\Rightarrow A< B\)
AY
19 tháng 5 2017
Ta có : \(A=\frac{1946}{1986};B=\frac{1968}{2008}\)
\(=>1-A=1-\frac{1946}{1986}=\frac{1986}{1986}-\frac{1946}{1986}=\frac{40}{1986}\)
\(=>1-B=1-\frac{1968}{2008}=\frac{2008}{2008}-\frac{1968}{2008}=\frac{40}{2008}\)
Vì \(\frac{40}{1986}>\frac{40}{2008}=>1-\frac{1946}{1986}>1-\frac{1968}{2008}\)
\(=>1-A>1-B\)
Từ đó suy ra : A < B
LH
5
18 tháng 4 2015
ta có \(A=\frac{1946}{1986}\)
\(\Rightarrow1-A=1-\frac{1946}{1986}=\frac{1986}{1986}-\frac{1946}{1986}=\frac{40}{1986}\)
\(\Rightarrow1-B=1-\frac{1968}{2008}=\frac{2008}{2008}-\frac{1968}{2008}=\frac{40}{2008}\)
Vì \(\frac{40}{1986}>\frac{40}{2008}\Rightarrow1-\frac{1946}{1986}>1-\frac{1968}{2008}\)
nên \(\Rightarrow1-A>1-B\left(1\right)\)
từ (1) <=> A<B
21 tháng 6 2020
Ta có: \(A=\frac{1946}{1986}=\frac{1986-40}{1986}=1-\frac{40}{1986}\)
\(B=\frac{1968}{2008}=\frac{2008-40}{2008}=1-\frac{40}{2008}\)
Ta có: \(\frac{40}{1986}>\frac{40}{2008}\)
\(\Rightarrow-\frac{40}{1986}< -\frac{40}{2008}\)
\(\Rightarrow-\frac{40}{1986}+1< \frac{-40}{2008}+1\)
hay A<B
24 tháng 4 2018
\(\frac{-1946}{1986}>\frac{-1968}{2008}\)
chúc bạn học tốt~
24 tháng 4 2018
TA SO SÁNH PHẦN BÙ CỚI 1 CỦA MỖI SỐ ĐÓ:
\(1-\frac{1946}{1986}=\frac{40}{1986}\) VÀ \(1-\frac{1968}{2008}=\frac{40}{2008}\) VÌ CÓ \(\frac{40}{1986}>\frac{40}{2008}\) NÊN \(\frac{1946}{1986}< \frac{1968}{2008}\)
20 tháng 4 2016
hai số có hiệu 40 . Phân số nào bé hơn số đó bé hơn . Vậy ta điền dấu <
CT
0
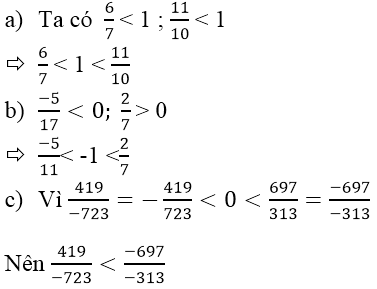
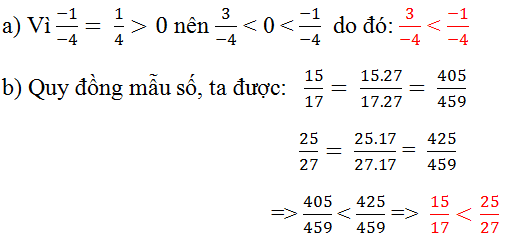
\(1=\dfrac{1946}{1986}+\dfrac{40}{1986}\)
\(1=\dfrac{1968}{2008}+\dfrac{40}{2008}\)
\(\Rightarrow\)\(\dfrac{40}{1968}>\dfrac{40}{2008}\)
\(\Rightarrow\dfrac{1946}{1968}>\dfrac{1968}{2008}\)
Vì \(\left\{{}\begin{matrix}1=\dfrac{1946}{1986}+\dfrac{40}{1986}\\1=\dfrac{1968}{2008}+\dfrac{40}{2008}\end{matrix}\right.\)
Mà \(\dfrac{40}{1986}>\dfrac{40}{2008}\)
Nên \(\dfrac{1946}{1986}>\dfrac{1968}{2008}\)
Vậy \(\dfrac{1946}{1986}>\dfrac{1968}{2008}\).