K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LM
Lê Minh Vũ
CTVHS
1 tháng 10 2021
Số học sinh chọn âm nhạc là :
\(55-20=35\) ( học sinh )
Số học sinh chọn thể thao là :
\(44-20=24\) ( học sinh )
Số học sinh không chọn môn nào là :
\(100-\left(35+24+20\right)=21\) ( học sinh )
1 tháng 10 2021
Ta có sơ đồ Ven sau :
55 44 20 Tổng số học sinh thi đỗ đại học Số học sinh chọn âm nhạc Số học sinh chọn cả 2 môn Số học sinh chọn thể thao
Khi đó số học sinh không chọn môn nào là :
100 - 55 - 44 + 20 = 21 ( học sinh )
Vậy có 21 học sinh không chọn cả hai môn
CM
20 tháng 2 2018
Ta có bảng phân bố tần số- tần suất ghép lớp sau:
| Lớp | [36;44) | [44;52) | [52;60) | [60;68) | [68;76) | [76;84) | Cộng |
Tần số |
3 |
6 |
6 |
8 |
3 |
4 |
30 |
Tần suất (%) |
10 |
20 |
20 |
26,7 |
10 |
13,3 |
100% |
Tần suất của L 4 lớn nhất.
CM
27 tháng 5 2018
Có 3+4+3+4+7+2+4=9 số liệu nằm trong nửa khoảng chiếm [40;8;79;2) chiếm 27 30 × 100 = 90 %
Chọn đáp án D.
CM
17 tháng 7 2017
Ta có bảng phân bố tần số-tần suất ghép lớp sau:
Lớp |
L 1 |
L 2 |
L 3 |
L 4 |
L 5 |
L 6 |
L 7 |
L 8 |
L 9 |
L 10 |
Cộng |
Tần số |
1 |
3 |
4 |
3 |
4 |
7 |
2 |
0 |
4 |
2 |
30 |
Tần suất (%) |
3,3 |
10 |
13,3 |
10 |
13,3 |
23,4 |
6,7 |
0 |
13,3 |
6,7 |
100% |
a) Diện tích cột với đáy [45,6;50,4) là ( 50,4 - 45, 6). 4 = 19,2.
Chọn B
CM
15 tháng 5 2019
Chọn B
Do kích thước mẫu N = 18 là số chẵn nên số trung vị là trung bình cộng của 2 giá trị đứng ở vị trí thứ 9 và thứ 10
CM
2 tháng 10 2019
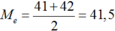
Chọn A.
Để tính số trung bình ta ghi lại số liệu theo bảng tần số:
Vậy số trung bình gần với số 42 nhất.
DT
0
NT
1
2 tháng 12 2017
ta có : \(sin136^0=sin\left(180-136\right)^0=sin44^0\left(đpcm\right)\)
ta có : \(cos136^0=-cos\left(180-136\right)^0=-cos44^0\left(đpcm\right)\)
