GN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
1
SI
7 tháng 7 2021
Ta có :
\(B=4+2^2+2^3+2^4+...+2^{2016}\)
\(\Rightarrow\) \(B-4=2^2+2^3+2^4+...+2^{2016}\)
\(\Rightarrow\) \(2\left(B-4\right)=2^3+2^4+2^5+...+2^{2017}\)
\(\Rightarrow\) \(2\left(B-4\right)-\left(B-4\right)=B-4=2^{2017}-2^2\)
\(\Rightarrow\) \(B=2^{2017}-2^2+4=2^{2017}\)
\(\Rightarrow\) \(A=B=2^{2017}\)
Vậy \(A=B\)
2
5 tháng 5 2022
`[x-3]/5=[2x-6]/10`
`[2(x-3)]/10=[2x-6]/10`
`2x-6=2x-6`
`2x-2x=-6+6`
`0x=0` (LĐ)
Vậy `x in RR`
KK
19 tháng 3 2022
(x+1)+(2x+3)+(3x+5)+...+(100x+199)=30200
=(x+2x+3x+..........+100x)+(1+3+5+......+199)=4950
=x.(1+2+3+.........+100)+(1+3+5+.......+199)=4950
=>5050x+10000=30200
=>5050x=30200-4950
=>5050x=25250
=>x=25250:5050
=>x=5
25 tháng 7 2018
i don't now
mong thông cảm !
...........................
U
25 tháng 7 2018
\(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}\)
ta có :
\(\frac{1}{2^2}< \frac{1}{1\cdot2}\)
\(\frac{1}{3^2}< \frac{1}{2\cdot3}\)
\(\frac{1}{4^2}< \frac{1}{3\cdot4}\)
...
\(\frac{1}{100^2}< \frac{1}{99\cdot100}\)
nên \(A< \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{99\cdot100}\)
\(\Rightarrow A< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(\Rightarrow A< 1-\frac{1}{100}\)
\(\Rightarrow A< \frac{99}{100}< 1\)
\(\Rightarrow A< 1\left(đpcm\right)\)
nhiều qá lm sao nổi
NA
8 tháng 2 2022
a : vì \(\dfrac{354}{758}< 1;\dfrac{123}{56}>1\\ \Rightarrow\dfrac{354}{758}< \dfrac{123}{56}\)
b:\(\dfrac{-18}{2021}< 0;\dfrac{75}{2022}>0\\ \Rightarrow\dfrac{-18}{2021}< \dfrac{75}{2022}\)
8 tháng 2 2022
a) Do 354/758<1 ;123/56>1
=>354/758<123/56
b) -18/2021<0;72/2022>0
=>-18/2021<72/2022
5 tháng 7 2016
2161 > 2160 = 24.40 = (24)40 = 1640 > 1340 nên 2161 > 1340.
5 tháng 7 2016
Ta giữ nguyên 1340
Ta thấy 2161>2160
.Mà 2160=24.40=(24)40=1640 Do 16>13 nên 1340<2161
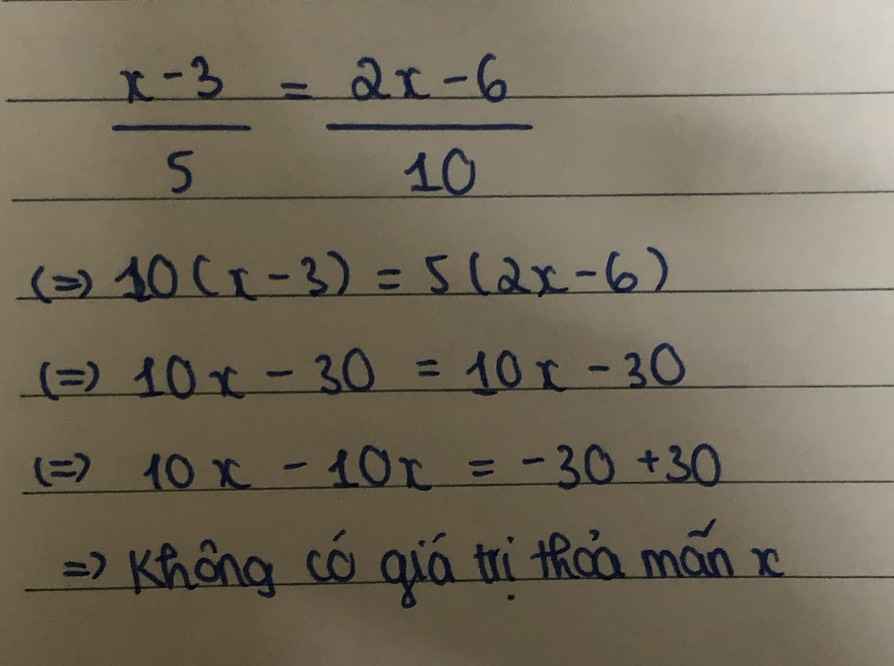
chắc là bé hơn