DS
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 10 2019
Gọi số cần tìm là \(\overline{abcd}\Rightarrow a>b>c>d\)
Với mỗi bộ 4 chữ số phân biệt lập ra từ \(\left\{0;1;2;...;9\right\}\) luôn có duy nhất 1 cách sắp xếp thỏa mãn yêu cầu bài toán
\(\Rightarrow\) Có \(C_{10}^4=210\) số thỏa mãn yêu cầu
//Ps: do a lớn nhất nên cứ yên tâm rằng ko bao giờ rơi vào trường hợp số 0 đứng đầu cả, chừng nào bài toán cho \(a< b< c< d\) lúc đó mới cần xét a
QD
31 tháng 3 2017
a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB của chúng trên mp(α)
Giả sử HA = HB
Vì SH ⊥ mp(α) nên SH ⊥ HA và SH ⊥ SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có canh SH chung và HA = HB nên :
ΔSHA = ΔSHB SA = SB
Ngược lại nếu SA = SB thì ΔSHA = ΔSHB ⇒ HA = HB
Kết quả, ta có HA = HB SA= SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(α) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B' sao cho HA' = HA ⇒ HC > HA'. Như vậy, theo kết quả câu a) ta có SA' = SA. Ta có trong các tam giác vuông SHB', SHC thì :
SC2= SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA' nên SC2 > SA2 ⇒ SC > SA
Suy ra SC > SA
Như vậy HC > HA ⇒ SC > SA
Lí luận tương tự, ta có : SC > SA ⇒ HC > HA
Kết quả : HC > HA ⇔ SC > SA
LH
31 tháng 3 2017
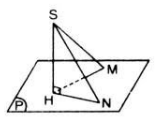
a) Gọi SN là một đường xiên khác. Xét hai tam giác vuông SHM và SHN có SH chung. Nếu SM = SN => tam giác SHM = tam giác SHN => HM = HN, ngược lại nếu HM = HN thì tam giác SHM = tam giác SHNSM => SM = SN.
b) Xét tam giác vuông SHM và SHN có SH chung. Nếu SN > SM thì \(HN^2-SN^2-SH^2\) => \(SM^2-SH^2=HM^2\) => HN > HM. Chứng minh tương tự cho chiều ngược lại.
CM
27 tháng 4 2017
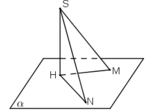
Giả sử ta có hai đường xiên SM, SN và các hình chiếu HM, HN của chúng trên mp (α).
Vì SH ⊥ mp(α)
⇒ SH ⊥ HM và SH ⊥ HN
⇒ ΔSHN và ΔSHM vuông tại H.
Áp dụng định lí Py-ta- go vào hai tam giác vuông này ta có:
⇒ S M 2 = S H 2 + H M 2 ; v à S N 2 = S H 2 + H N 2 . a ) S M = S N ⇔ S M 2 = S N 2 ⇔ H M 2 = H N 2 ⇔ H M = H N . b ) S M > S N ⇔ S M 2 > S N 2 ⇔ H M 2 > H N 2 ⇔ H M > H N .
HB
2
11 tháng 5 2016
Số các chữ số tự nhiên có 4 chữ số lớn hơn 2014 là :
( 9999 - 2015 ) : 1 + 1 = 7985 ( số )
Đáp số 7985 số
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2020
a/ Với mỗi bộ 5 chữ số phân biệt bất kì, có duy nhất 1 cách sắp xếp chúng theo thứ tự giảm dần
\(\Rightarrow\) Có \(C_{10}^5=252\) số thỏa mãn
b/ Gọi số đó là \(\overline{abcde}\) \(\Rightarrow1\le a< b< c< d< e\) và \(e\) lẻ
\(\Rightarrow e\ge5\)
- Với \(e=5\Rightarrow\overline{abcd}\) có đúng 1 cách chọn (1234)
- Với \(e=7\Rightarrow\overline{abcd}\) chọn bằng cách lấy 4 số từ 6 số (1;2;...6) \(\Rightarrow C_6^4=15\) cách
- Với \(e=9\Rightarrow\) có \(C_8^4=70\) số
Vậy có: \(1+15+70=86\) số thỏa mãn
EM CHƯA HỌC 11
oo+1 nha