K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 10 2023
46:
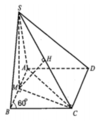
(SAB) và (SAD) cùng vuông góc (ABCD)
=>SA vuông góc (ABCD)
=>SA vuông góc AC
ΔSAC vuông tại A
=>\(SC=\sqrt{AS^2+AC^2}=a\sqrt{2}\)
\(V=\dfrac{1}{3}\cdot SA\cdot S_{ABCD}=\dfrac{1}{3}\cdot a\sqrt{2}\cdot a^2=\dfrac{a^3\sqrt{2}}{3}\)
=>Chọn C
47:
\(\dfrac{V_{BC.A'B'C'}}{V_{ABC.A'B'C'}}=\dfrac{2}{3}\)
=>V1=2/3*V
=>Chọn A
48:
AB vuông góc AC
AB vuông góc AD
Do đó: AB vuông góc (ACD)
\(V_{ABCD}=\dfrac{1}{3}\cdot AB\cdot S_{ACD}=\dfrac{1}{3}\cdot5\cdot\dfrac{1}{2}\cdot12\cdot10=100\)
=>Chọn A
CM
4 tháng 11 2017
Chọn A.
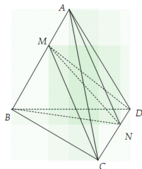
Nhìn vào hình vẽ ta thấy MN là giao tuyến của hai mặt phẳng (MCD) và (NAB), khi đó ta thấy tứ diện đã cho được chia thành bốn tứ diện ACMN, AMND, BMNC, BMND.
CM
25 tháng 2 2018
Chọn A.
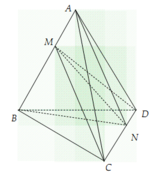
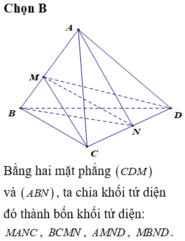
Nhìn vào hình vẽ ta thấy MN là giao tuyến của hai mặt phẳng (MCD) và (NAB), khi đó ta thấy tứ diện đã cho được chia thành bốn tứ diện ACMN,AMND,BMNC,BMND.
47,5 nhé
Là số 47,5 nha !