Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Chọn 2 trong 10 học sinh chia thành nhóm 2 có: 
cách
Chọn 3 trong 8 học sinh còn lại chia thành nhóm 3 có: 
cách
Chọn 5 trong 5 học sinh còn lại chia thành nhóm 5 có: 
cách
Vậy có 
cách.
Đáp án C
Số cách xếp ngẫu nhiên là 10! cách.=
Ta tìm số cách xếp thoả mãn:
* Trước tiên xếp 2 học sinh lớp A có 2! cách.
Vì giữa hai học sinh lớp A không có học sinh lớp B nên chỉ có thể xếp học sinh lớp C vào giữa hai học sinh lớp A vừa xếp:
* Vậy chọn k ∈ 0 , 1 , 2 , 3 , 4 , 5 học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có A 5 k cách, ta được một nhóm X.
* Xếp 10 - (2+k) = 8- k học sinh còn lại với nhóm X có (9 -k)! cách.
Vậy tất cả có ∑ 2 k = 0 5 ! A 5 k ( 9 - k ) ! = 1451520 cách xếp thỏa mãn
Xác suất cần tính bằng 1451520 10 ! = 2 5
Chọn C
Số cách xếp ngẫu nhiên là 10! cách.
Ta tìm số cách xếp thoả mãn:
* Trước tiên xếp 2 học sinh lớp A có 2! cách.
Vì giữa hai học sinh lớp A không có học sinh lớp B nên chỉ có thể xếp học sinh lớp C vào giữa hai học sinh lớp A vừa xếp:
* Vậy chọn 
học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có
A
5
k
cách, ta được một nhóm X.
* Xếp 
học sinh còn lại với nhóm X có (9-k)! cách.
Vậy tất cả có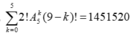 
cách xếp thỏa mãn.
Xác suất cần tính bằng 
Xếp 10 bạn theo thứ tự bất kì: \(10!\) cách
Số cách xếp 5 bạn nam xen kẽ 5 bạn nữ: \(2.\left(5!\right)^2\)
Số cách thỏa mãn: \(10!-2.\left(5!\right)^2=...\)
a) \(100+98+96+...+2-97-95-93-...-3\)
= \(100+98+\left(96-97\right)+\left(94-95\right)+...+\left(2-3\right)\)
= \(100+98-95\) = \(103\)
b) \(2-4-6+8+10-12-14+16+...-102+104\)
= \(\left(2-4\right)+\left(-6+8\right)+\left(10-12\right)+\left(-14+16\right)+...+\left(-102+104\right)\)
= \(-2+2-2+2-2+...+2\) = \(0\)
c) \(1+2-3-4+5+6-7-8+9+10-11-12+...-111-112+113+114\)
= \(\left(1+2\right)-\left(3+4\right)+\left(5+6\right)-\left(7+8\right)+...\left(113+114\right)\)
= \(3-7+11-15+19-23+...+219-223+227\)
= \(\left(3-7\right)+\left(11-15\right)+\left(19-23\right)+...+\left(219-223\right)+227\)
= \(-4-4-4-4-...-4+227\)
= \(54\left(-4\right)+227\) = \(-216+227\) = \(11\)
Chọn 2 trong 10 học sinh chia thành nhóm 2 người có: C 10 2 cách.
Chọn 3 trong 8 học sinh còn lại chia thành nhóm 3 người có: C 8 3 cách.
Chọn 5 trong 5 học sinh còn lại chia thành nhóm 5 có C 5 5 cách.
Vậy có C 10 2 . C 8 3 . C 5 5 cách.
Chọn đáp án B