Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).

y = \(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\)
y = \(\dfrac{sin^2x}{sinx.cosx-cos^2x}+\dfrac{1}{4}=\dfrac{\dfrac{sin^2x}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}-1}+\dfrac{1}{4}\)
y = \(\dfrac{tan^2x}{tanx-1}+\dfrac{1}{4}\)
y = \(\dfrac{4tan^2x+tanx-1}{4tanx-4}\). Đặt t = tanx. Do x ∈ \(\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\) nên t ∈ (1 ; +\(\infty\))\
Ta đươc hàm số f(t) = \(\dfrac{4t^2+t-1}{4t-4}\)
⇒ ymin = \(\dfrac{17}{4}\) khi t = 2. hay x = arctan(2) + kπ

b:
ĐKXĐ: \(\left\{{}\begin{matrix}cosx< >0\\sinx< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< >\dfrac{\Omega}{2}+k\Omega\\x\ne k\Omega\end{matrix}\right.\)
=>\(x\ne\dfrac{\Omega}{2}+\dfrac{k\Omega}{2}\)
\(\dfrac{1}{cosx}+\dfrac{\sqrt{3}}{sinx}=2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot\left[sinx\cdot\cos\dfrac{\Omega}{3}+sin\left(\dfrac{\Omega}{3}\right)\cdot cosx\right]\)
=>\(\dfrac{sinx+\sqrt{3}\cdot cosx}{cosx\cdot sinx}=2\cdot\left(\dfrac{1}{2}\cdot sinx+\dfrac{\sqrt{3}}{2}\cdot cosx\right)\)
=>\(\left(sinx+\sqrt{3}\cdot cosx\right)\left(\dfrac{1}{cosx\cdot sinx}-1\right)=0\)
=>\(2\cdot\left(sinx\cdot\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\cdot cosx\right)\cdot\left(\dfrac{2}{2\cdot sinx\cdot cosx}-1\right)=0\)
=>\(2\cdot sin\left(x+\dfrac{\Omega}{3}\right)\cdot\left(\dfrac{2}{sin2x}-1\right)=0\)
=>\(\left[{}\begin{matrix}sin\left(x+\dfrac{\Omega}{3}\right)=0\\\dfrac{2}{sin2x}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=k\Omega\\sin2x=2\left(loại\right)\end{matrix}\right.\)
=>\(x=-\dfrac{\Omega}{3}+k\Omega\)

sin π/6 = 1/2; cos π/6 = √3/2
sin π/4 = √2/2; cos π/4 = √2/2
sin 1,5 = 0,9975; cos 1,5 = 0,0707
sin 2 = 0,9093; cos 2 = -0,4161
sin 3,1 = 0,0416; cos 3,1 = -0,9991
sin 4,25 = -0,8950; cos 4,25 = -0,4461
sin 5 = -0,9589; cos 5 = 0,2837
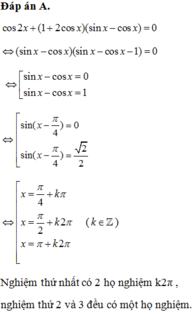
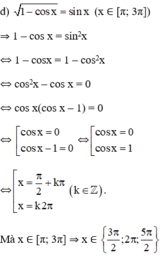
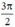 không thỏa mãn
không thỏa mãn
Vậy thì bạn phải biết đọc đường tròn lượng giác
Mà đừng hỏi mình đọc đường tròn lượng giác thế nào nhé, cái đấy SGK viết rất rõ rồi