S
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 6 2023
a: -10/8<-1
-19/19=-1
-1<-2/10<0
0<5/12<1<17/15
=>17/15>1>5/12>-2/10>-19/19>-10/8
b: -1/3=-4/12; -5/12=-5/12; -3/4=-9/12; -1/4=-3/12; -7/12=-7/12
=>-3/4<-7/12<-5/12<-1/3<-1/4
31 tháng 3 2018
Gọi A = -1+x4+2x4+7x-6x4-3x
=>A = -1+(x4-6x4+2x4)+(7x-3x)
=>A = -1+(-3x4)+4x
Sắp xếp ta có :
A = -3x4+4x-1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
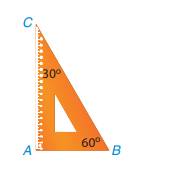
- AB < AC < BC nên sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn là: AB, AC, BC.
\(\widehat C < \widehat B < \widehat A\) nên sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn là: \(\widehat C;\widehat B;\widehat A\)
- Góc lớn nhất là góc A đối diện với cạnh BC. Góc bé nhất là góc C đối diện với cạnh AB.
TD
2
IM
27 tháng 8 2016
Ta có
\(2^{100}=\left(2^4\right)^{25}=16^{25}\)
\(3^{75}=\left(3^3\right)^{25}=27^{25}\)
\(5^{50}=\left(5^2\right)^{25}=25^{25}\)
Vì \(16^{25}< 25^{25}< 27^{25}\)
\(\Rightarrow2^{100}< 5^{50}< 3^{75}\)
Vậy sắp xếp \(2^{200};5^{50};3^{75}\)
10 tháng 5 2017
Vì tổng ba góc trong 1 tam giác bằng 1800
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
hay 600 + 500 + \(\widehat{C}=180^0\)
=> \(\widehat{C}=180^0-110^0=70^0\)
Ta có : \(\widehat{C}>\widehat{A}>\widehat{B}\left(70^0>60^0>50^0\right)\)
\(\Leftrightarrow AB>BC>AC\)
hay AC < BC < AB
LT
10 tháng 5 2017
độ dài góc C là
180-50-60=70
vì góc A đối diện với cạnh BC
góc B đối diện với cạnh AC
góc C đối diện với cạnh AB
ma goc C>A>B =>AB>BC>AC=>AC<BC<AB
mk nah bn
1/2;4/5;4/7;7/4
k mình nha chúc cậu học tốt