Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi chiều rộng = a => chiều dài = a+10
Áp dụng định lý Pytago => a^2 + (a+10)^2 = độ dài đường chéo ^2 = 1300
=> 2a^2 +20a +100=1300
=> a^2 +10a-600 = 0
=> (a+30)(a-20) =0
=> a=20
=> chu vi sân bóng = 2(a+a+10) = 2.50 =100

Đây là sân bóng đá mini hình chữ nhật
gọi chiều dài là x m( x>0)
chiều rộng là x/2 m
theo đề ra ta có phương trình
2(x+x/2)=120
<=> x+x/2=60
<=> 3x=120
<=>x=40
vậy chiều dài sân bóng là 40
chiều rộng sânn bóng là 20
diện tích sân bóng là 40*20=800 m^2

Gọi chiều dài và chiều rộng của sân bóng lần lượt là \(x,y\left(m\right);x,y>0\).
Vì chu vi là \(140m\)nên \(2\left(x+y\right)=140\Leftrightarrow x+y=70\)
Vì giảm chiều rộng đi \(5m\)tăng chiều dài thêm \(8m\)thì diện tích sân bóng không đổi nên
\(\left(x+8\right)\left(y-5\right)=xy\Leftrightarrow-5x+8y=40\)
Ta có hệ phương trình:
\(\hept{\begin{cases}x+y=70\\-5x+8y=40\end{cases}}\Leftrightarrow\hept{\begin{cases}5x+5y=350\\-5x+8y=40\end{cases}}\Leftrightarrow\hept{\begin{cases}x=40\\y=30\end{cases}}\)(thỏa mãn)
Vậy chiều dài là \(40m\)chiều rộng là \(30m\).

Nửa chu vi hình chữ nhật: 194 : 2 = 97 (m)
Gọi chiều dài là: x (m) (0 < x < 97)
Chiều rộng là: y (m) (0 < x < 97)
Nửa chu vi là 97 nên ta có phương trình:
x + y = 97 (1)
4 lần chiều dài hơn 5 lần chiều rộng là 10m, nên ta có phương trình:
4x - 5y = 10 (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=97\\4x-5y=10\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=55\left(TM\right)\\y=42\left(TM\right)\end{matrix}\right.\)
Vậy chiều dài và chiều rộng sân trường lần lượt là: 55m và 42m

Gọi chiều dài là a (m), hiều rộng là b(m)
Có a+b=140 : 2=70 (m)
Chiều dài sau khi tăng là a+8 (m)
chiều rộng sai khi giảm là b-5 (m)
Có hệ ptr a+b=70 (1)
(a+8)(b-5)=ab (2)
(2) <=> 8b-5a-40=0
<=>8b-5a=40
(1)<=> a=70-b
=> (2) <=> 8b+5b-350=40
<=>13b=390
<=>b=30(m)
=> a=40(m)
<=>43b=390

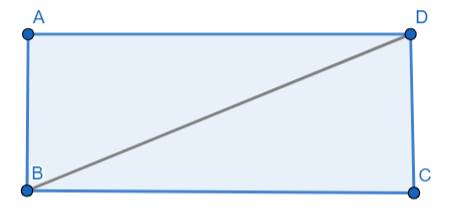
Ta có: \(AD=3AB\)
Xét tam giác vuông ABD ta có:
\(AD^2+AB^2=BD^2\)
\(\Rightarrow60^2=\left(3AB\right)^2+AB^2\)
\(\Rightarrow3600=9AB^2+AB^2\)
\(\Rightarrow3600=10AB^2\)
\(\Rightarrow AB^2=360\)
\(\Rightarrow AB=6\sqrt{10}\left(m\right)\)
\(\Rightarrow AD=3\cdot6\sqrt{10}=18\sqrt{10}\left(m\right)\)
Diện tích sân bóng là:
\(AB\cdot AD=6\sqrt{10}\cdot18\sqrt{10}=1080\left(m^2\right)\)

Khó lắm cậu tự giải đi nhé hihi
Chi phí rào quanh sân là
260 000×72 =18 720 000 (đ)
Vậy chi phí là 18 720 000 đ