Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\sqrt{\dfrac{25}{81}.\dfrac{16}{49}.\dfrac{196}{9}}=\sqrt{\dfrac{25}{81}}.\sqrt{\dfrac{16}{49}}.\sqrt{\dfrac{196}{9}}=\dfrac{5}{9}.\dfrac{4}{7}.\dfrac{14}{3}=\dfrac{40}{27}\)
b) \(\sqrt{3\dfrac{1}{16}.2\dfrac{14}{25}.2\dfrac{34}{81}}=\sqrt{\dfrac{49}{16}.\dfrac{64}{25}.\dfrac{196}{81}}=\sqrt{\dfrac{49}{16}}.\sqrt{\dfrac{64}{25}}.\sqrt{\dfrac{196}{81}}=\dfrac{7}{4}.\dfrac{8}{5}.\dfrac{14}{9}=\dfrac{196}{45}\)
c) \(\dfrac{\sqrt{640}.\sqrt{34,3}}{\sqrt{567}}=\sqrt{\dfrac{640.34,3}{567}}=\sqrt{\dfrac{64.49}{81}}=\dfrac{\sqrt{64}.\sqrt{49}}{\sqrt{81}}=\dfrac{8.7}{9}=\dfrac{56}{9}\)
d) \(\sqrt{21,6}.\sqrt{810}.\sqrt{11^2-5^2}=\sqrt{21,6.810.\left(11^2-5^2\right)}=\sqrt{216.81.\left(11+5\right)\left(11-5\right)}=\sqrt{36^2.9^2.4^2}=36.9.4=1296\)

Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.
Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.

a) ĐS: .
b) ĐS: Nếu thì
Nếu ab
c) ĐS:
d)
Nhận xét. Nhận thấy rằng để có nghĩa thì
Do đó
. Vì thế có thể phân tích tử thành nhân tử.
a) ĐS: .
b) ĐS: Nếu thì
Nếu ab
c) ĐS:
d)
Nhận xét. Nhận thấy rằng để có nghĩa thì
Do đó
. Vì thế có thể phân tích tử thành nhân tử.

a ) \(\dfrac{2}{\sqrt{3}-1}\) - \(\dfrac{2}{\sqrt{3}+1}\) = \(\dfrac{2\left(\sqrt{3}+1\right)-2\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
= \(\dfrac{2\sqrt{3}+2-2\sqrt{3}+2}{3-1}\) = \(\dfrac{4}{2}\) = 2
b) \(\dfrac{5}{12\left(2\sqrt{5}+3\sqrt{2}\right)}\) - \(\dfrac{5}{12\left(2\sqrt{5}-3\sqrt{2}\right)}\)
= \(\dfrac{5\left(2\sqrt{5}-3\sqrt{2}\right)-5\left(2\sqrt{5}+3\sqrt{2}\right)}{12\left(2\sqrt{5}+3\sqrt{2}\right)\left(2\sqrt{5}-3\sqrt{2}\right)}\)
= \(\dfrac{10\sqrt{5}-15\sqrt{2}-10\sqrt{5}-15\sqrt{2}}{12\left(20-18\right)}\)
= \(\dfrac{-30\sqrt{2}}{24}\) = \(\dfrac{-15\sqrt{2}}{12}\) = \(\dfrac{-5\sqrt{2}}{4}\)
c) \(\dfrac{5+\sqrt{5}}{5-\sqrt{5}}\) +\(\dfrac{5-\sqrt{5}}{5+\sqrt{5}}\) = \(\dfrac{\left(5+\sqrt{5}\right)^2+\left(5-\sqrt{5}\right)^2}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)
= \(\dfrac{25+10\sqrt{5}+5+25-10\sqrt{5}+5}{25-5}\) = \(\dfrac{60}{20}\) = 3
d) \(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3+1}}-1}\) - \(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3+1}}+1}\)
= \(\dfrac{\sqrt{3}}{\sqrt{2}-1}\) - \(\dfrac{\sqrt{3}}{\sqrt{2}+1}\) = \(\dfrac{\sqrt{3}\left(\sqrt{2}+1\right)-\sqrt{3}\left(\sqrt{2}-1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}\)
= \(\dfrac{\sqrt{6}+\sqrt{3}-\sqrt{6}+\sqrt{3}}{2-1}\) = \(2\sqrt{3}\)

a) \(\left(\sqrt{8}-3\sqrt{2}+\sqrt{10}\right)\sqrt{2}-\sqrt{5}=\sqrt{16}-6+\sqrt{20}-\sqrt{5}=4-6+2\sqrt{5}-\sqrt{5}=\sqrt{5}-2\)
b) \(0,2\sqrt{\left(-10\right)^3.3}+2\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}=0,2\left|-10\right|\sqrt{3}+2\left|\sqrt{3}-\sqrt{5}\right|=0,2.10.\sqrt{3}+2\left(\sqrt{5}-\sqrt{3}\right)=2\sqrt{3}+2\sqrt{5}-2\sqrt{3}=2\sqrt{5}\)
c) \(\left(\dfrac{1}{2}\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{200}\right):\dfrac{1}{8}=\left(\dfrac{1}{2}\sqrt{\dfrac{2}{4}}-\dfrac{3}{2}\sqrt{2}+8\sqrt{2}\right):\dfrac{1}{8}=\left(\dfrac{1}{4}\sqrt{2}-\dfrac{2}{3}\sqrt{2}+8\sqrt{2}\right):\dfrac{1}{8}=\dfrac{27}{4}\sqrt{2}.8=54\sqrt{2}\)
d) \(2\sqrt{\left(\sqrt{2}-3\right)^2}+\sqrt{2.\left(-3\right)^2}-5\sqrt{\left(-1\right)^4}=2\left(3-\sqrt{2}\right)+3\sqrt{2}-5=6-2\sqrt{2}+3\sqrt{2}-5=1+\sqrt{2}\)

\(A=\frac{1}{\sqrt{1}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{5}}+...+\frac{1}{\sqrt{23}+\sqrt{25}}\)
\(2A=\frac{2}{\sqrt{3}+\sqrt{1}}+\frac{2}{\sqrt{5}+\sqrt{3}}+...+\frac{2}{\sqrt{25}+\sqrt{23}}\)\(2A=\frac{2\left(\sqrt{3}-\sqrt{1}\right)}{\left(\sqrt{3}+\sqrt{1}\right)\left(\sqrt{3}-\sqrt{1}\right)}+\frac{2\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}+...+\frac{2\left(\sqrt{25}-\sqrt{23}\right)}{\left(\sqrt{25}+\sqrt{23}\right)\left(\sqrt{25}-\sqrt{23}\right)}\)
\(2A=\frac{2\left(\sqrt{3}-\sqrt{1}\right)}{2}+\frac{2\left(\sqrt{5}-\sqrt{3}\right)}{2}+...+\frac{2\left(\sqrt{25}-\sqrt{23}\right)}{2}\)
\(2A=\sqrt{3}-\sqrt{1}+\sqrt{5}-\sqrt{3}+\sqrt{25}-\sqrt{23}\)
\(2A=\sqrt{25}-\sqrt{1}\)
\(2A=4\)
\(A=2\)
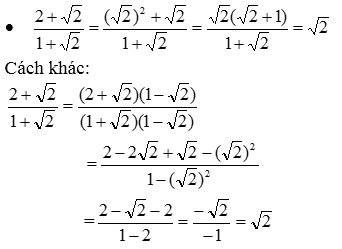
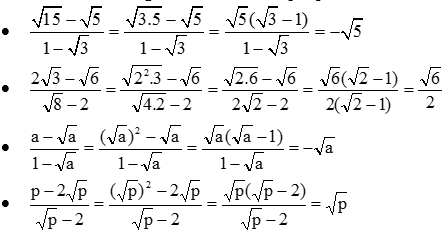
\(3\sqrt{144}-5\sqrt{49}+\dfrac{1}{2}\sqrt{36}\)
\(=3.12-5.7+\dfrac{1}{2}.6\)
\(=36-35+3=4\)