
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{2}\sqrt{48}-2\sqrt{75}-\frac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\frac{1}{3}}\)
=\(\frac{1}{2}\sqrt{3.4^2}-2\sqrt{3.5^2}-\sqrt{\frac{33}{11}}+5\sqrt{\frac{4}{3}}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+10\sqrt{\frac{1}{3}}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\frac{10}{3}\sqrt{3}\)
\(=\left(2-10-1+\frac{10}{3}\right)\sqrt{3}\)
\(=\frac{-17}{3}\sqrt{3}\)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4,5\sqrt{2\frac{2}{3}}-\sqrt{6}\)
\(=\sqrt{6.5^2}+\sqrt{96}+4,5\sqrt{\frac{8}{3}}-\sqrt{6}\)
\(=5\sqrt{6}+\sqrt{6.4^2}+4,5\frac{\sqrt{24}}{3}-\sqrt{6}\)
\(=5\sqrt{6}+4\sqrt{6}+\frac{4,5.2\sqrt{6}}{3}-\sqrt{6}\)
\(=8\sqrt{6}+3\sqrt{6}\)
\(=11\sqrt{6}\)
Tự hòi tự trl :D ?
\(\frac{1}{2}\sqrt{48}-2\sqrt{75}-\frac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\frac{1}{3}}\)
\(=\frac{1}{2}\sqrt{16.3}-2.5\sqrt{3}-\sqrt{3}-\frac{10}{3}\sqrt{3}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}-\frac{10}{3}\sqrt{3}\)
\(=-9\sqrt{3}+\frac{10}{3}\sqrt{3}=\left(-9+\frac{10}{3}\right)\sqrt{3}\)
\(=-\frac{17}{3}\sqrt{3}\)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4,5.\sqrt{2\frac{2}{3}}-\sqrt{6}\)
\(=\sqrt{25.6}+\sqrt{1,6.60}+4,8\sqrt{\frac{8}{3}}-\sqrt{6}\)
\(=5\sqrt{6}+\sqrt{16.6}+4,5.\frac{1}{3}\sqrt{3^2.\frac{4.2}{3}}-\sqrt{6}\)
\(=9\sqrt{6}+3\sqrt{6}-\sqrt{6}=11\sqrt{6}\)

a) \(ĐKXĐ:x\ne4;x\ne9\)
b) \(A=\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}-\frac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\frac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\frac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\frac{-\sqrt{x}+x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
c) Ta có: \(A=\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{\left(\sqrt{x}-3\right)+4}{\sqrt{x}-3}=1+\frac{4}{\sqrt{x}-3}\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\) (ĐK: x thuộc Z)
| \(\sqrt{x}-3\) | 1 | -1 | 2 | -2 | 4 | -4 |
| \(\sqrt{x}\) | 4 | 2 | 5 | 1 | 7 | -1 |
| x | 2 | \(\sqrt{2}\) | \(\sqrt{5}\) | \(\sqrt{1}\) | \(\sqrt{7}\) | \(\varnothing\) |
Vậy để A thuộc Z khi x = {2;\(\sqrt{2};\sqrt{5};\sqrt{1};\sqrt{7}\) }

a. \(C=\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}-\frac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\frac{2\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}-\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\frac{2\sqrt{x}-9-\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
b. C=\(\frac{\sqrt{x}+1}{\sqrt{x}-3}=1+\frac{4}{\sqrt{x}-3}\)
C nguyên \(\Leftrightarrow\sqrt{x}-3\inƯ\left(4\right)\Rightarrow\sqrt{x}-3\in\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{1;2;4;5;7\right\}\Rightarrow x\in\left\{1;4;16;25;49\right\}\)
Vậy \(x\in\left\{1;4;16;25;49\right\}\)thì C nguyên
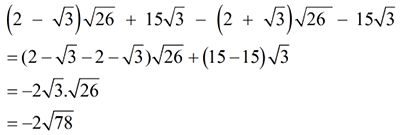

\(\sqrt{\frac{3}{5}}+\sqrt{\frac{5}{3}}-\frac{1}{2}\sqrt{60}\)
\(=\frac{\sqrt{3}}{\sqrt{5}}+\frac{\sqrt{5}}{\sqrt{3}}-\sqrt{\frac{1}{4}\cdot60}\)
\(=\frac{\sqrt{15}}{5}+\frac{\sqrt{15}}{3}-\sqrt{15}\)
\(=\frac{3\sqrt{15}}{15}+\frac{5\sqrt{15}}{15}-\frac{15\sqrt{15}}{15}=\frac{-7\sqrt{15}}{15}\)