Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Cách 1 :
\(M=\sqrt{11-6\sqrt{2}}+\sqrt{11+6\sqrt{2}}\)
\(M=\sqrt{9-6\sqrt{2}+2}+\sqrt{9+6\sqrt{2}+2}\)
\(M=\sqrt{\left(3-\sqrt{2}\right)^2}+\sqrt{\left(3+\sqrt{2}\right)^2}\)
\(M=\left|3-\sqrt{2}\right|+\left|3+\sqrt{2}\right|\)
\(M=3-\sqrt{2}+3+\sqrt{2}=6\)
Cách 2 :
\(M=\sqrt{11-6\sqrt{2}}+\sqrt{11+6\sqrt{2}}\)
\(\Rightarrow M^2=11-6\sqrt{2}+2\sqrt{11-6\sqrt{2}}.\sqrt{11+6\sqrt{2}}+11+6\sqrt{2}\)
\(\Leftrightarrow M^2=22+2.7=36\)
\(\Leftrightarrow M=6\left(\sqrt{11-6\sqrt{2}}+\sqrt{11+6\sqrt{2}}>0\right)\)
2)
\(A=53-20\sqrt{4+\sqrt{9-4\sqrt{2}}}\)
\(\Leftrightarrow A=53-20\sqrt{4+\sqrt{8-4\sqrt{2}+1}}\)
\(\Leftrightarrow A=53-20\sqrt{4+\sqrt{\left(2\sqrt{2}-1\right)^2}}\)
\(\Leftrightarrow A=53-20\sqrt{4+\left|2\sqrt{2}-1\right|}\)
\(\Leftrightarrow A=53-20\sqrt{4+2\sqrt{2}-1}\)
\(\Leftrightarrow A=53-20\sqrt{3+2\sqrt{2}}\)
\(\Leftrightarrow A=53-20\sqrt{2+2\sqrt{2}+1}\)
\(\Leftrightarrow A=53-20\left(\sqrt{2}+1\right)\)
\(\Leftrightarrow A=53-20\sqrt{2}-20=33-20\sqrt{2}\)
3)
\(M=\sqrt{3-\sqrt{5}}.\left(3+\sqrt{5}\right)\left(\sqrt{10}-\sqrt{2}\right)\)
\(M=\sqrt{3-\sqrt{5}}.\left(3\sqrt{10}-3\sqrt{2}+5\sqrt{2}-\sqrt{10}\right)\)
\(M=\sqrt{3-\sqrt{5}}\left(2\sqrt{10}+2\sqrt{2}\right)\)
\(M=2\sqrt{2}.\sqrt{3-\sqrt{5}}\left(\sqrt{5}+1\right)\)
\(\Rightarrow M^2=8.\left(3-\sqrt{5}\right).\left(5+2\sqrt{5}+1\right)\)
\(\Leftrightarrow M^2=\left(24-8\sqrt{5}\right)\left(6+2\sqrt{5}\right)\)
\(\Leftrightarrow M^2=144+48\sqrt{5}-48\sqrt{5}-80\)
\(\Leftrightarrow M^2=64\Leftrightarrow M=8\left(\sqrt{3-\sqrt{5}}.\left(3+\sqrt{5}\right).\left(\sqrt{10}-\sqrt{2}\right)>0\right)\)

=\(\sqrt{3}-1+2-\) \(\sqrt{3}=1\)
b.=\(\frac{2+\sqrt{3}-2+\sqrt{3}}{2^2-3}=2\sqrt{3}\)

a) \(\left(2\sqrt{3}+\sqrt{5}\right)\sqrt{3}-\sqrt{60}\) = \(6+\sqrt{15}-2\sqrt{15}\)
= \(6-\sqrt{15}\)
b) \(\left(5\sqrt{2}+2\sqrt{5}\right)\sqrt{5}-\sqrt{250}\) = \(5\sqrt{10}+10-5\sqrt{10}\) = \(10\)
c) \(\left(\sqrt{28}-\sqrt{12}-\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\) = \(14-2\sqrt{21}-7+2\sqrt{21}\)
= \(7\)
d) \(\left(\sqrt{99}-\sqrt{18}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)
= \(33-3\sqrt{22}-11+3\sqrt{22}\) = \(22\)
a)(2√3+√5)√3-√60
=6+√15-2√15
=6-√15
b)(5√2+2√5)√5-√250
=5√10+10-5√10
=10
c)(√28-√12-√7)√7+2√21
=14-2√21-7+2√21
=7
d)(√99-√18-√11)√11+3√22
=33-3√22-11+3√22
=22

1. Câu hỏi của Nữ hoàng sến súa là ta - Toán lớp 9 - Học toán với OnlineMath

b, \(\frac{\sqrt{3}}{2+\sqrt{3}}-\frac{\sqrt{3}}{2-\sqrt{3}}\) = \(\frac{\sqrt{3}\left(2-\sqrt{3}\right)-\sqrt{3}\left(2+\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)=\(\frac{2\sqrt{3}-3-2\sqrt{3}-3}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)=\(\frac{-6}{4-3}\)=-6
c,\(\frac{2}{\sqrt{5}-2}-\frac{2}{\sqrt{5}+2}\)=\(\frac{2\left(\sqrt{5}+2\right)-2\left(\sqrt{5}-2\right)}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}\)=\(\frac{2\sqrt{5}+4-2\sqrt{5}+4}{\sqrt{5}^2-2^2}\)=\(\frac{8}{1}\)=8

\(=\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(2\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}+2-2\sqrt{3}+1\)
\(=3-\sqrt{3}\)
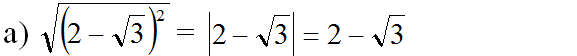
Lời giải:
$\sqrt{0,169}+\sqrt{0,25}-\sqrt{(-11)^2}$
$=\sqrt{0,13^2.10}+\sqrt{0,5^2}-\sqrt{(-11)^2}$
$=|0,13|\sqrt{10}+|0,5|-|-11|$
$=0,13\sqrt{10}+0,5-11=0,13\sqrt{10}-10,5$