Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\frac{\left(a+2\right)^2\left(5a-15a^2\right)}{\left(a-3\right)\left(4a-a^3\right)}=\frac{\left(a+2\right)^2.5a.\left(1-3a\right)}{\left(a-3\right).a.\left(2-a\right)\left(a+2\right)}\)
\(=\frac{\left(a+2\right).5.\left(1-3a\right)}{\left(a-3\right).\left(2-a\right)}\)

a: \(A=25a^2+50a+25+10\left(a^2-2a-3\right)+a^2-6a+9\)
\(=26a^2+46a+34+10a^2-20a-30\)
\(=36a^2+26a+4\)
b: \(B=\dfrac{1}{4}\left(x^2-2x+1\right)+x^2-1+x^2+2x+1\)
\(=\dfrac{1}{4}x^2-\dfrac{1}{2}x+\dfrac{1}{4}+2x^2+2x\)
\(=\dfrac{9}{4}x^2+\dfrac{3}{2}x+\dfrac{1}{4}\)

a)\(\dfrac{12x^3y^2}{18xy^5}\)=\(\dfrac{2x^2}{3y^3}\)
b)\(\dfrac{15x.\left(x+5\right)^2}{20x^2.\left(x+5\right)}\)=\(\dfrac{3.5x\left(x+5\right)}{4x.5x.\left(x+5\right)}\)=\(\dfrac{3\left(x+5\right)}{4x}\)

a) \(\dfrac{20+10a+5a^2}{a^3-8}=\dfrac{5\left(a^2+2a+4\right)}{\left(a-2\right)\left(a^2+2a+4\right)}=\dfrac{5}{a-2}\)
b) \(\dfrac{x\left(2-x\right)}{x^2-5x+6}=\dfrac{-x\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{-x}{x-3}=\dfrac{x}{3-x}\)
c) \(\dfrac{y^2-x^2}{x^2-3xy+2y^2}=\dfrac{\left(y-x\right)\left(y+x\right)}{\left(x-y\right)\left(x-2y\right)}=\dfrac{x+y}{2y-x}\)

a, Xét tử thức \(x^2\left(y-z\right)+y^2\left(z-x\right)+z^2\left(x-y\right)\)
\(=x^2\left(y-z\right)-y^2\left(x-z\right)+z^2\left[\left(x-z\right)-\left(y-z\right)\right]\)
\(=x^2\left(y-z\right)-y^2\left(x-z\right)+z^2\left(x-z\right)-z^2\left(y-z\right)\)
\(=\left(x^2-z^2\right)\left(y-z\right)-\left(y^2-z^2\right)\left(x-z\right)\)
\(=\left(x-z\right)\left(x+z\right)\left(y-z\right)-\left(y-z\right)\left(y+z\right)\left(x-z\right)\)
\(=\left(x-z\right)\left(xy-xz+yz-z^2-y^2-yz+yz+z^2\right)\)
\(=\left(x-z\right)\left(xy-xz+yz-y^2\right)=\left(x-z\right)\left[x\left(y-z\right)-y\left(y-z\right)\right]\)
\(=\left(x-z\right)\left(x-y\right)\left(y-z\right)\)
Mẫu thức \(x^2y-x^2z+y^2z-y^3=x^2\left(y-z\right)-y^2\left(y-z\right)=\left(x-y\right)\left(x+y\right)\left(y-z\right)\)
Vậy \(\frac{x^2\left(y-z\right)+y^2\left(z-x\right)+z^2\left(x-y\right)}{x^2y-x^2z+y^2z-y^3}=\frac{\left(x-y\right)\left(y-z\right)\left(x-z\right)}{\left(x-y\right)\left(x+y\right)\left(y-z\right)}=\frac{x-z}{x+y}\)
b, \(\frac{x^5+x+1}{x^3+x^2+x}=\frac{x^5-x^2+x^2+x+1}{x\left(x^2+x+1\right)}=\frac{x^2\left(x-1\right)\left(x^2+x+1\right)+x^2+x+1}{x\left(x^2+x+1\right)}=\frac{\left(x^2+x+1\right)\left(x^3-x^2+1\right)}{x\left(x^2+x+1\right)}=\frac{x^3-x^2+1}{x}\)

\(a,\frac{\left(2x^2+2x\right)\left(x-2\right)^2}{\left(x^3-4x\right)\left(x+1\right)}\)
\(=\frac{2x\left(x+1\right)\left(x-2\right)^2}{x\left(x-2\right)\left(x+2\right)\left(x+1\right)}\)
\(=\frac{2\left(x-2\right)}{x+2}\)
Với \(x=\frac{1}{2}\)
\(\Rightarrow\frac{2\left(x-2\right)}{x+2}=\frac{2\left(\frac{1}{2}-2\right)}{\frac{1}{2}+2}=\frac{2.-\frac{3}{2}}{\frac{5}{2}}=-3.\frac{2}{5}=\frac{-6}{5}\)
b,Do x = -5; y = 10=> y = -2x
Thay y = -2x vào biểu thức ta được
\(\frac{x^3-x^2\left(-2x\right)+x\left(-2x\right)^2}{x^3+\left(-2x\right)^3}\)
\(=\frac{x^3+2x^3+2x^2}{x^3-8x^3}\)
\(=\frac{3x^3+2x^2}{-7x^3}=\frac{3}{-7}+\frac{2}{-7x}\)
Thay x = -5 là đc
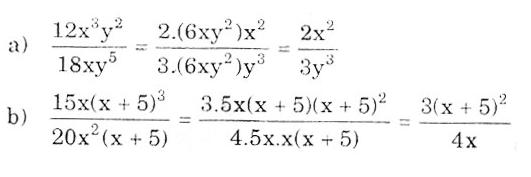

\(\dfrac{5a^2\left(a+b\right)^3}{10a\left(a+b\right)^2}=\dfrac{a\left(a+b\right)}{2}\)
\(\dfrac{5a^2\left(a+b\right)^3}{10a\left(a+b\right)^2}=\dfrac{a\left(a+b\right)}{2}\)