Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(a,x^2+4x-21-x^2-4x+5=-16\\ b,=\left(x+8-x+2\right)^2=10^2=100\\ c,=x^2\left(x^2-16\right)-\left(x^4-1\right)\\ =x^4-16x^2-x^4+1=1-16x^2\\ d,=x^3+1-x^3+1=2\)
\(a,=x^2+4x-21-x^2-4x+5=-16\\ b,=\left(x+8-x+2\right)^2=10^2=100\\ c,=x^2\left(x^2-16\right)-\left(x^4-1\right)\\ =x^4-16x^2-x^4+1=1-16x^2\\ d,=x^3+1-x^3+1=2\)
Bài 1:
\(a,=15x^4-12x^3+9x^2\\ b,=-15x^3y^2+25x^2y^2-5xy^3\\ c,=5x^3-15x^2-4x^2+12x=5x^3-19x^2+12x\\ d,=3x^3-9x^2y+xy^2-3y^3+5x^2y-15xy^2=3x^3-3y^3-4x^2y-14xy^2\)
Bài 2:
\(a,=x^2+4x-21-x^2-4x+5=-16\\ b,=x^2+16x+64-2x^2-12x+32+x^2-4x+4=100\\ c,=x^4-16x^2-x^4+1=1-16x^2\\ d,=x^3+1-x^3+1=2\)
a kham khảo nha , e nhờ a e lm chứ ko phải e lm nha !
\(\left(x-2\right)\left(\frac{3}{x}+2-\frac{5}{2x}-4+\frac{8}{x^2}-4\right)\)
\(\left(x-2\right)\left[\left(\frac{3}{x}-\frac{5}{2x}\right)-6+\frac{8}{x^2}\right]\)
\(\left(x-2\right)\left(\frac{1}{2x}-6+\frac{8}{x^2}\right)\)
\(\left(x-2\right)\left(\frac{3}{x+2}-\frac{5}{2x-4}+\frac{8}{x^2-4}\right)\)
\(=\left(x-2\right)\left[\frac{3}{x+2}-\frac{5}{2\left(x-2\right)}+\frac{8}{\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{3.2\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}-\frac{5\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\frac{8.2}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{6\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}-\frac{5\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\frac{16}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{6\left(x-2\right)-5\left(x+2\right)+16}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\frac{\left(x-2\right)\left(x-6\right)}{2\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x-6}{2\left(x+2\right)}\)
\(1,\left(x+y\right)^2-\left(x-y\right)^2=\left[\left(x+y\right)-\left(x-y\right)\right]\left[\left(x+y\right)+\left(x-y\right)\right]=\left(x+y-x+y\right)\left(x+y+x-y\right)=2y.2x=4xy\)
\(2,\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
\(3,\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =4y^2\)
\(4,\left(2x+3\right)^2-2\left(2x+3\right)\left(2x+5\right)+\left(2x+5\right)^2\\ =\left[\left(2x+3\right)-\left(2x+5\right)\right]^2\\ =\left(2x+3-2x-5\right)^2\\ =\left(-2\right)^2\\ =4\)
\(5,9^8.2^8-\left(18^4+1\right)\left(18^4-1\right)\\ =18^8-\left[\left(18^4\right)^2-1\right]\\ =18^8-18^8+1\\ =1\)
1: =x^2+2xy+y^2-x^2+2xy-y^2=4xy
2: =x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3
=6x^2y
3: =(x+y-x+y)^2=(2y)^2=4y^2
4: =(2x+3-2x-5)^2=(-2)^2=4
5: =18^8-18^8+1=1
a) (6x+1)2 + (6x-1)2 - 2(1+6x)(6x-1)
= (6x+1+6x-1)2
=144x2
b) x(2x2 -3) - x2(5x+1) +x2
=2x3 - 3x - 5x3 -x2+x2
=-3x3-3x
=-3x(x2+1)
c) 3(22+1)(24+1)(28+1)(216+1)
= (22-1)(22+1)(24+1)(28+1)(216+1)
= (24-1)(24+1)(28+1)(216+1)
= (28-1)(28+1)(216+1)
= (216-1)(216+1)
= 232 -1
d) 3x(x-2) - 5x(1-x) - 8(x2 -3)
= 3x2-6x - 5x + 5x2 - 8x2 +24
= -11x +24
Bài 8:
Ta có: \(A=-x^2+2x+4\)
\(=-\left(x^2-2x-4\right)\)
\(=-\left(x^2-2x+1-5\right)\)
\(=-\left(x-1\right)^2+5\le5\forall x\)
Dấu '=' xảy ra khi x=1
\(a,\left(x-1\right)^2-2^2=\left(x-1-2\right)\left(x-1+2\right)=\left(x-3\right)\left(x+1\right)\\ b,=\left(2x\right)^2+2.2x.3+3^2\\ =\left(2x+3\right)^2\\ c,=x^3-\left(2y\right)^3\\ =\left(x-2y\right)\left(x^2+2xy+4y^2\right)\\ d,=x^3\left(x^2-1\right)-\left(x^2-1\right)\\ =\left(x^3-1\right)\left(x^2-1\right)\\ =\left(x-1\right)\left(x^2+x+1\right)\left(x-1\right)\left(x+1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2+x+1\right)\)
\(e,=-4x^2\left(x-1\right)+\left(x-1\right)\\ =\left(1-4x^2\right)\left(x-1\right)\\ =\left(1-2x\right)\left(1+2x\right)\left(x-1\right)\)
\(f,=\left(2x\right)^3+3.\left(2x\right)^2.1+3.2x.1^2+1^3\\ =\left(2x+1\right)^3\)
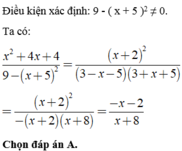
a, \(\frac{x^{32}+x^{16}+1}{x^{16}+x^8+1}\)
\(=\frac{x^8+x^4+1}{x^4+x^2+1}\) Vậy phân thức \(a=\frac{x^8+x^4+1}{x^4+x^2+1}\)
P/s; Căn thức a, là phân số tối giản
b, \(\frac{x^8+3x^4+4}{x^4+x^2+2}\)
\(=\frac{x^4+3x^2+2}{x^2+x^1+1}\) Vậy căn thức \(b=\frac{x^4+3x^2+2}{x^2+x^1+1}\)
P/s; Căn thức b, có thể rút gọn được cho 2 và 4
Em ko chắc đâu nhé *-*
