
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


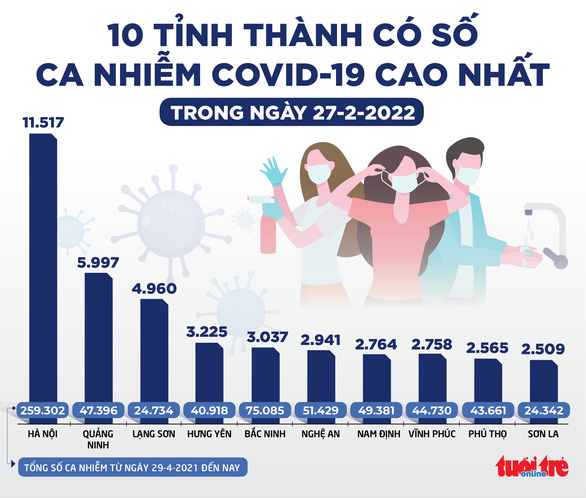
a. Những tỉnh thành phố có ca nhiễm hơn 2800 ca: Nghệ An, Bắc Ninh, Hưng Yên, Lạng Sơn, Quảng Ninh, Hà Nội.
b. Tỉnh có số ca nhiễm Covid 19 cao nhất là: Hà Nội


\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

Lời giải:
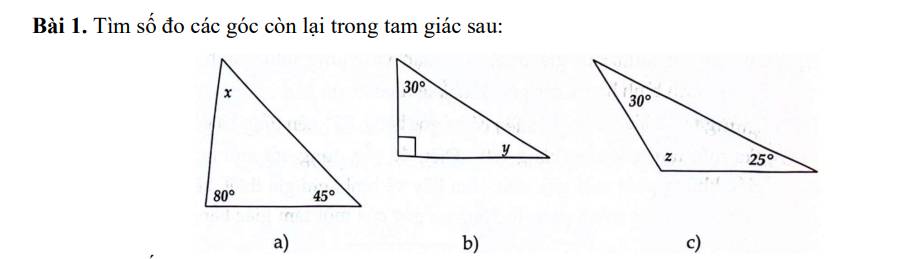
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$

\(a)\hept{\begin{cases}\text{Ta có:}\widehat{A_4}=\widehat{B_2}=110^0\\\text{Mà chúng so le trong}\end{cases}}\)
\(\Rightarrow a//b\)
\(b)\hept{\begin{cases}\text{Ta có:}c\perp a\left(gt\right)\\\text{Mà }a//b\left(cmt\right)\end{cases}}\)
\(\Rightarrow c\perp b\)
\(c)\text{Ta có:}\widehat{B_1}+\widehat{B_2}=180^0\left(\text{kề bù}\right)\)
\(\Rightarrow\widehat{B_1}=180^0-\widehat{B_2}\)
\(\Rightarrow\widehat{B_1}=180^0-110^0=70^0\)
\(\text{Ta có:}\widehat{B_1}=\widehat{B_3}=70^0\left(\text{đối đỉnh}\right)\)
\(\text{Ta có:}\widehat{B_3}=\widehat{C_3}\left(\text{Đồng vị}\right)\)
\(\Rightarrow\widehat{B_3}=\widehat{C_3}=70^0\)
a) Ta có: {ˆA4=110∘ˆB2=110∘⇒ˆA4=ˆB2=110∘{A4^=110∘B2^=110∘⇒A4^=B2^=110∘.
Mà hai góc ờ vị trí so le trong ⇒⇒ a//ba//b.
b) Ta có: {c⊥aa//b⇒c⊥b{c⊥aa//b⇒c⊥b
c) Vì a//b⇒ˆA4+ˆB1=180∘a//b⇒A4^+B1^=180∘
Mà hai góc ở vị trí trong cùng phía ⇒ˆB1=180∘−ˆA4=70∘⇒B1^=180∘−A4^=70∘.
Vì b⊥cb⊥c; e⊥ce⊥c và b//eb//e
⇒ˆB2=ˆC2=110∘⇒B2^=C2^=110∘ (hai góc ở vị trí đồng vị)
Ta có ˆC2C2^ và ˆC3C3^ là hai góc kề bù ⇒ˆC2+ˆC3=180∘⇒C2^+C3^=180∘
⇒ˆC3=180∘−ˆC2=70∘⇒C3^=180∘−C2^=70∘.

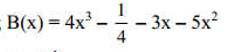
 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!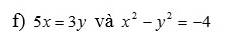


Đơn thức đã được rút gọn rồi bạn nhé.