K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 9 2021
\(A=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\left(x\ge0;x\ne1\right)\\ A=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{15\sqrt{x}-11-3x-7\sqrt{x}+6-2x-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\dfrac{-\left(5\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}\)
NM
2
31 tháng 7 2016
BC = 5 cm
violympic mà cx phải giải chi tiết ak??
45645764575678768769780845735732156364576576587687
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
Lời giải:
\(\frac{2x-2\sqrt{x}+2}{x-\sqrt{x}}=\frac{2(x-\sqrt{x})+2}{x-\sqrt{x}}=\frac{2(x-\sqrt{x})+2}{x-\sqrt{x}}=2+\frac{2}{x-\sqrt{x}}\)
4 tháng 9 2021
\(\dfrac{2x-2\sqrt{x}+2}{x\sqrt{x}+1}=\dfrac{2}{\sqrt{x}+1}\)
NN
2
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 9 2023
Tuỳ vào bài đó như thế nào
Có những bài có độ chính xác cao em nên giữ nguyên kết quả
Nhưng nguyên tắc làm tròn thì 4,9014 thì làm tròn xuống 4,9 thui chứ không làm tròn lên 5 nha
Y
11 tháng 4 2022
Mk ra đáp án khác với đáp án ủa bn nên bn bào sai chứ j, thật ra cả 2 đáp án đều giống nhau, do biến đổi dấu nên trở thành 2 đáp án khác nhau thôi :V
để mk lm lại phần đáp án của mk ra giống đáp án của bn nek :V
\(a,\)\(P=\dfrac{-x-1}{x-1}\)
\(\Rightarrow\dfrac{-\left(-x-1\right)}{-\left(x-1\right)}=\dfrac{x-1}{-x+1}=\dfrac{x-1}{1-x}\)
Còn câu b thì hôm qua bn ghi là \(x=\dfrac{1}{\sqrt{2}}\) chứ có pk là \(1\sqrt{2}\) đou >:V
\(b,\)Thay \(x=1\sqrt{2}\) vào \(P\) ta có :
\(P=\dfrac{x-1}{1-x}\)
\(P=\dfrac{1\sqrt{2}-1}{1-1\sqrt{2}}=3+2\sqrt{2}\)
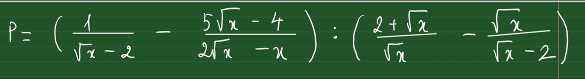
\(P=\dfrac{\sqrt{x}+5\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}:\dfrac{x-4-x}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{6\sqrt{x}-4}{-4}=\dfrac{2-3\sqrt{x}}{2}\)
\(P=\left(\dfrac{1}{\sqrt{x}-2}+\dfrac{5\sqrt{x}-4}{x-2\sqrt{x}}\right):\left(\dfrac{2+\sqrt{x}}{\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}-2}\right)\)
\(=\dfrac{2\left(3\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}:\dfrac{x-4-x}{\left(\sqrt{x}-2\right)\cdot\sqrt{x}}\)
\(=\dfrac{-3\sqrt{x}+2}{2}\)