
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{11+6\sqrt{2}}=\sqrt{\left(3+\sqrt{2}\right)^2}=3+\sqrt{2}\)

Rút gọn biểu thức
A=Căn ((2 căn 10 + căn 30 - 2 căn 2 - căn 6)/(2 căn 10 - 2 căn 2)) ÷ 2/ ( căn 3 -1)



\(\sqrt{\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}}+\sqrt{\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}}\)
\(=\sqrt{\dfrac{\left(\sqrt{3}-\sqrt{2}\right)^2}{3-2}}+\sqrt{\dfrac{\left(\sqrt{3}+\sqrt{2}\right)^2}{3-2}}\)
\(=\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}=2\sqrt{3}\)

Bài 1:
a) \(B=\sqrt{1-4x+4x^2}\)
\(=\sqrt{\left(1-2x\right)^2}\)
\(=\left|1-2x\right|\)
Nếu \(x\le\frac{1}{2}\)thì: \(B=1-2x\)
Nếu \(x>\frac{1}{2}\)thì: \(B=2x-1\)
b) Tại \(x=-7\)thì: \(B=1-2.\left(-7\right)=15\)
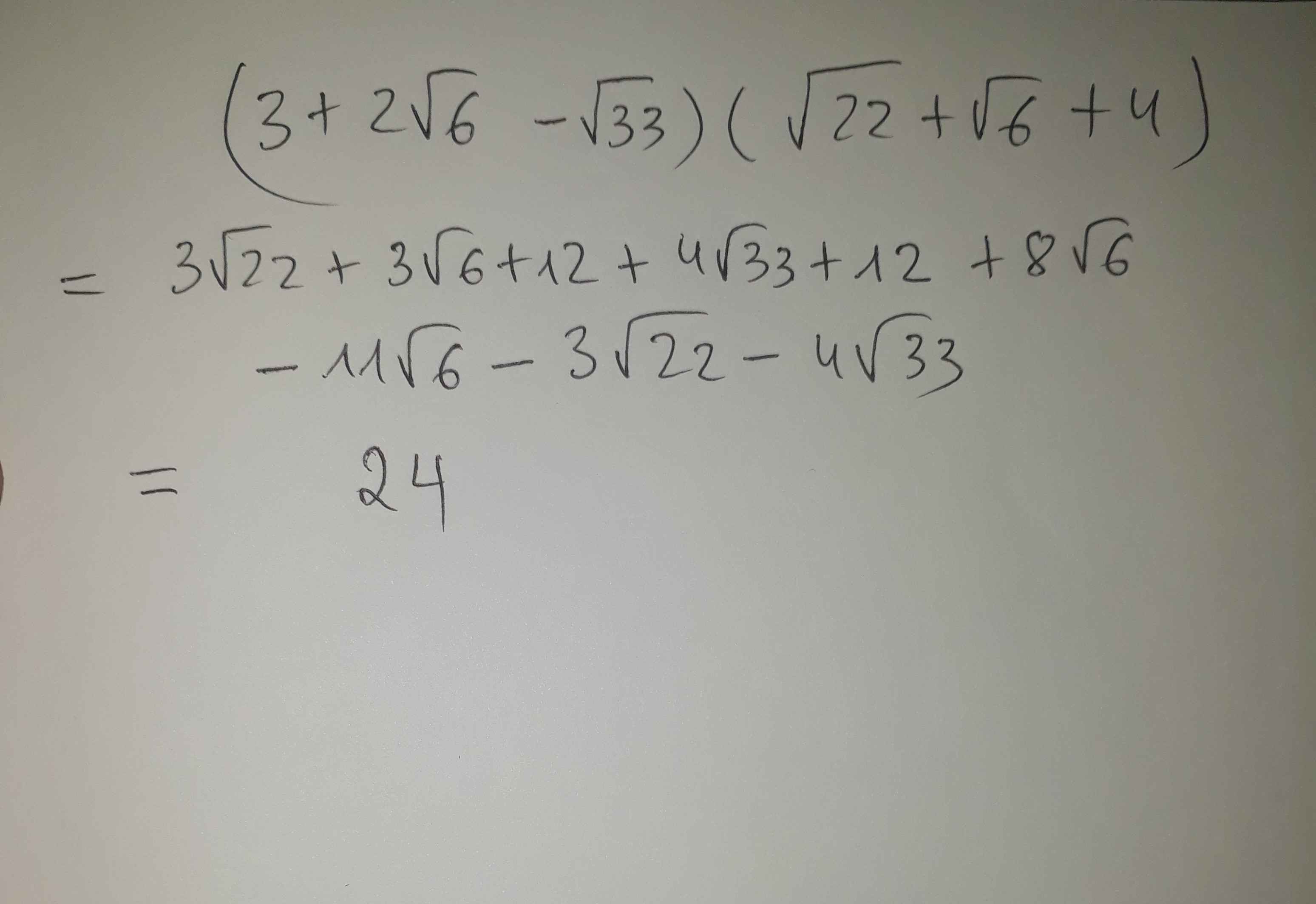
\(\sqrt{11+6\sqrt{2}}-3+\sqrt{2}=\sqrt{\left(3+\sqrt{2}\right)^2}-3+\sqrt{2}=3+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}\)
\(\sqrt{11+6\sqrt{2}}-3+\sqrt{2}\)
\(=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)