K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 11 2021
\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện
23 tháng 4 2021
\(\frac{1}{3-\sqrt{7}}-\frac{1}{3+\sqrt{7}}=\frac{3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}-\frac{3-\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}\)
\(=\frac{3+\sqrt{7}-3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}=\frac{2\sqrt{7}}{9-7}=\sqrt{7}\)
23 tháng 4 2021
a, \(\frac{1}{3-\sqrt{7}}-\frac{1}{3+\sqrt{7}}=\frac{3+\sqrt[]{7}-3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}\)
\(=\frac{2\sqrt{7}}{9-7}=\sqrt{7}\)
F
20 tháng 8 2021
1.
A= \(2\sqrt{6}\) + \(6\sqrt{6}\) - \(8\sqrt{6}\)
A= 0
2.
A= \(12\sqrt{3}\) + \(5\sqrt{3}\) - \(12\sqrt{3}\)
A= 0
3.
A= \(3\sqrt{2}\) - \(10\sqrt{2}\) + \(6\sqrt{2}\)
A= -\(\sqrt{2}\)
4.
A= \(3\sqrt{2}\) + \(4\sqrt{2}\) - \(\sqrt{2}\)
A= \(6\sqrt{2}\)
5.
M= \(2\sqrt{5}\) - \(3\sqrt{5}\) + \(\sqrt{5}\)
M= 0
6.
A= 5 - \(3\sqrt{5}\) + \(3\sqrt{5}\)
A= 5
This literally took me a while, pls sub :D
https://www.youtube.com/channel/UC4U1nfBvbS9y_Uu0UjsAyqA/featured
25 tháng 6 2021
`(sqrt{24}+sqrt{75}-3)/(2sqrt{14}+sqrt{175}-sqrt{21})`
`=(sqrt3(sqrt8+sqrt25-sqrt3))/(sqrt7(2sqrt2+sqrt{25}-sqrt3))`
`=sqrt3/sqrt7`
`=sqrt{3/7}`
`**sqrt8=sqrt{4.2}=2sqrt2`
AT
25 tháng 6 2021
\(\dfrac{\sqrt{24}+\sqrt{75}-3}{2\sqrt{14}+\sqrt{175}-\sqrt{21}}=\dfrac{2\sqrt{3}.\sqrt{2}+5\sqrt{3}-3}{2\sqrt{2}.\sqrt{7}+5\sqrt{7}-\sqrt{3}.\sqrt{7}}\)
\(=\dfrac{\sqrt{3}\left(2\sqrt{2}+5-\sqrt{3}\right)}{\sqrt{7}\left(2\sqrt{2}+5-\sqrt{3}\right)}=\dfrac{\sqrt{3}}{\sqrt{7}}=\dfrac{\sqrt{21}}{7}\)
20 tháng 8 2021
\(\sqrt{16b}+2\sqrt{40b}-3\sqrt{90b}\)
\(=4\sqrt{b}+4\sqrt{10b}-9\sqrt{10b}\)
\(=4\sqrt{b}-5\sqrt{10b}\)
28 tháng 8 2021
b: Ta có: \(E=\dfrac{2}{\sqrt{3}-1}-\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{3}+1-\sqrt{3}+1\)
=2
c: ta có: \(F=\dfrac{\sqrt{15}-\sqrt{10}}{\sqrt{3}-\sqrt{2}}+\dfrac{3}{2-\sqrt{5}}\)
\(=\sqrt{5}-\sqrt{5}-2\)
=-2
26 tháng 8 2021
Bài 8:
Ta có: \(A=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2\cdot\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)^2}{4a}\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{a-1}{4a}\cdot\dfrac{-4\sqrt{a}}{1}\)
\(=\dfrac{-a+1}{\sqrt{a}}\)
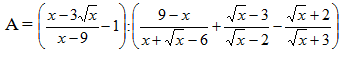
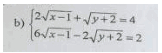
Rút gọn biểu thức
a) \(\sqrt{\left(1+2\sqrt{3}\right)^2}-5\sqrt{3}\)
= \(\left|1+2\sqrt{3}\right|-5\sqrt{3}\)
= \(1+2\sqrt{3}-5\sqrt{3}=1-3\sqrt{3}\)
b) \(3\sqrt{2}+4\sqrt{8}-\sqrt{18}\)
= \(3\sqrt{2}+4\sqrt{2.4}-\sqrt{2.9}\)
= \(3\sqrt{2}+8\sqrt{2}-3\sqrt{2}\) = \(8\sqrt{2}\)
a)\(\sqrt{\left(1+2\sqrt{3}\right)^2}-5\sqrt{3}=1+2\sqrt{3}-5\sqrt{3}=1-3\sqrt{3}\)
b)\(3\sqrt{2}-4\sqrt{8}-\sqrt{18}=3\sqrt{2}-8\sqrt{2}-3\sqrt{2}=-8\sqrt{2}\)
c)\(\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}=\dfrac{6}{5}\)