Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\frac{1}{\sqrt{1}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{5}}+...+\frac{1}{\sqrt{23}+\sqrt{25}}\)
\(2A=\frac{2}{\sqrt{3}+\sqrt{1}}+\frac{2}{\sqrt{5}+\sqrt{3}}+...+\frac{2}{\sqrt{25}+\sqrt{23}}\)\(2A=\frac{2\left(\sqrt{3}-\sqrt{1}\right)}{\left(\sqrt{3}+\sqrt{1}\right)\left(\sqrt{3}-\sqrt{1}\right)}+\frac{2\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}+...+\frac{2\left(\sqrt{25}-\sqrt{23}\right)}{\left(\sqrt{25}+\sqrt{23}\right)\left(\sqrt{25}-\sqrt{23}\right)}\)
\(2A=\frac{2\left(\sqrt{3}-\sqrt{1}\right)}{2}+\frac{2\left(\sqrt{5}-\sqrt{3}\right)}{2}+...+\frac{2\left(\sqrt{25}-\sqrt{23}\right)}{2}\)
\(2A=\sqrt{3}-\sqrt{1}+\sqrt{5}-\sqrt{3}+\sqrt{25}-\sqrt{23}\)
\(2A=\sqrt{25}-\sqrt{1}\)
\(2A=4\)
\(A=2\)

đkxđ a>=0 a khác 1
\(C=\left(\frac{a}{\sqrt{a}\left(\sqrt{a}-1\right)}-\frac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\frac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}+\frac{2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\right)\)
\(C=\frac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\frac{\sqrt{a}+3}{a-1}\)
\(C=\frac{\left(a-1\right).\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+3\right)}\)
b)
\(a=4-2\sqrt{3}=3-2\sqrt{3}+1=\left(\sqrt{3}-1\right)^2\)
\(\sqrt{a}=\sqrt{3}-1\)
thay vào nha
c) \(C=\frac{\left(a-1\right).\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+3\right)}\)
để c<0 thì \(\frac{\left(a-1\right).\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+3\right)}< 0\)
mà \(\sqrt{a}\left(\sqrt{a}+3\right)>0\)
\(\left(a-1\right)\left(\sqrt{a}+1\right)< 0\)
mà \(\sqrt{a}+1>0\)
nên a-1<0
\(0\le a< 1\)

Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.
Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.

a) ĐS: .
b) ĐS: Nếu thì
Nếu ab
c) ĐS:
d)
Nhận xét. Nhận thấy rằng để có nghĩa thì
Do đó
. Vì thế có thể phân tích tử thành nhân tử.
a) ĐS: .
b) ĐS: Nếu thì
Nếu ab
c) ĐS:
d)
Nhận xét. Nhận thấy rằng để có nghĩa thì
Do đó
. Vì thế có thể phân tích tử thành nhân tử.

a ) \(\dfrac{2}{\sqrt{3}-1}\) - \(\dfrac{2}{\sqrt{3}+1}\) = \(\dfrac{2\left(\sqrt{3}+1\right)-2\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
= \(\dfrac{2\sqrt{3}+2-2\sqrt{3}+2}{3-1}\) = \(\dfrac{4}{2}\) = 2
b) \(\dfrac{5}{12\left(2\sqrt{5}+3\sqrt{2}\right)}\) - \(\dfrac{5}{12\left(2\sqrt{5}-3\sqrt{2}\right)}\)
= \(\dfrac{5\left(2\sqrt{5}-3\sqrt{2}\right)-5\left(2\sqrt{5}+3\sqrt{2}\right)}{12\left(2\sqrt{5}+3\sqrt{2}\right)\left(2\sqrt{5}-3\sqrt{2}\right)}\)
= \(\dfrac{10\sqrt{5}-15\sqrt{2}-10\sqrt{5}-15\sqrt{2}}{12\left(20-18\right)}\)
= \(\dfrac{-30\sqrt{2}}{24}\) = \(\dfrac{-15\sqrt{2}}{12}\) = \(\dfrac{-5\sqrt{2}}{4}\)
c) \(\dfrac{5+\sqrt{5}}{5-\sqrt{5}}\) +\(\dfrac{5-\sqrt{5}}{5+\sqrt{5}}\) = \(\dfrac{\left(5+\sqrt{5}\right)^2+\left(5-\sqrt{5}\right)^2}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)
= \(\dfrac{25+10\sqrt{5}+5+25-10\sqrt{5}+5}{25-5}\) = \(\dfrac{60}{20}\) = 3
d) \(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3+1}}-1}\) - \(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3+1}}+1}\)
= \(\dfrac{\sqrt{3}}{\sqrt{2}-1}\) - \(\dfrac{\sqrt{3}}{\sqrt{2}+1}\) = \(\dfrac{\sqrt{3}\left(\sqrt{2}+1\right)-\sqrt{3}\left(\sqrt{2}-1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}\)
= \(\dfrac{\sqrt{6}+\sqrt{3}-\sqrt{6}+\sqrt{3}}{2-1}\) = \(2\sqrt{3}\)

b: \(=\dfrac{\left|x\right|+\left|x-2\right|+1}{2x-1}=\dfrac{x+x-2+1}{2x-1}=\dfrac{2x-1}{2x-1}=1\)
c: \(=\left|x-4\right|+\left|x-6\right|\)
=x-4+6-x=2

a: \(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{x-1}=\dfrac{-2\left(\sqrt{x}-1\right)}{x-1}=\dfrac{-2}{\sqrt{x}+1}\)
b: \(=\dfrac{\sqrt{x}-x\sqrt{y}-\sqrt{y}+y\sqrt{x}+\sqrt{x}+x\sqrt{y}+\sqrt{y}+y\sqrt{x}}{1-xy}:\left(\dfrac{x+y+2xy+1-xy}{1-xy}\right)\)
\(=\dfrac{2\sqrt{x}+2y\sqrt{x}}{1-xy}\cdot\dfrac{1-xy}{x+y+xy+1}\)
\(=\dfrac{2\sqrt{x}\left(y+1\right)}{\left(y+1\right)\left(x+1\right)}=\dfrac{2\sqrt{x}}{x+1}\)
c: \(=\dfrac{3x+3\sqrt{x}-9+x+2\sqrt{x}-3-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3x+5\sqrt{x}-8}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{3\sqrt{x}+8}{\sqrt{x}+2}\)

a) \(\left(\sqrt{8}-3\sqrt{2}+\sqrt{10}\right)\sqrt{2}-\sqrt{5}=\sqrt{16}-6+\sqrt{20}-\sqrt{5}=4-6+2\sqrt{5}-\sqrt{5}=\sqrt{5}-2\)
b) \(0,2\sqrt{\left(-10\right)^3.3}+2\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}=0,2\left|-10\right|\sqrt{3}+2\left|\sqrt{3}-\sqrt{5}\right|=0,2.10.\sqrt{3}+2\left(\sqrt{5}-\sqrt{3}\right)=2\sqrt{3}+2\sqrt{5}-2\sqrt{3}=2\sqrt{5}\)
c) \(\left(\dfrac{1}{2}\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{200}\right):\dfrac{1}{8}=\left(\dfrac{1}{2}\sqrt{\dfrac{2}{4}}-\dfrac{3}{2}\sqrt{2}+8\sqrt{2}\right):\dfrac{1}{8}=\left(\dfrac{1}{4}\sqrt{2}-\dfrac{2}{3}\sqrt{2}+8\sqrt{2}\right):\dfrac{1}{8}=\dfrac{27}{4}\sqrt{2}.8=54\sqrt{2}\)
d) \(2\sqrt{\left(\sqrt{2}-3\right)^2}+\sqrt{2.\left(-3\right)^2}-5\sqrt{\left(-1\right)^4}=2\left(3-\sqrt{2}\right)+3\sqrt{2}-5=6-2\sqrt{2}+3\sqrt{2}-5=1+\sqrt{2}\)

a/ Ta có:
\(\dfrac{1}{\sqrt{n+1}+\sqrt{n}}=\dfrac{\left(\sqrt{n+1}-\sqrt{n}\right)}{\left(\sqrt{n+1}+\sqrt{n}\right)\left(\sqrt{n+1}-\sqrt{n}\right)}=\sqrt{n+1}-\sqrt{n}\)
\(\Rightarrow A=\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}+...+\sqrt{2019}-\sqrt{2018}=\sqrt{2019}-1\)
a.\(A=\dfrac{1}{\sqrt{2}+1}+\dfrac{1}{\sqrt{3}+\sqrt{2}}+\dfrac{1}{\sqrt{4}+\sqrt{3}}+...+\dfrac{1}{\sqrt{2019}+\sqrt{2018}}=\dfrac{\sqrt{2}-1}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}+\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)}+...+\dfrac{\sqrt{2019}-\sqrt{2018}}{\left(\sqrt{2019}+\sqrt{2018}\right)\left(\sqrt{2019}-\sqrt{2018}\right)}=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+...+\sqrt{2019}-\sqrt{2018}=\sqrt{2019}-1\)

1/ Rút gọn: \(a)3\sqrt{2a}-\sqrt{18a^3}+4\sqrt{\dfrac{a}{2}}-\dfrac{1}{4}\sqrt{128a}\left(a\ge0\right)=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-2\sqrt{2a}=3\sqrt{2a}\left(1-a\right)\)b)\(\dfrac{\sqrt{2}-1}{\sqrt{2}+2}-\dfrac{2}{2+\sqrt{2}}+\dfrac{\sqrt{2}+1}{\sqrt{2}}=\dfrac{\sqrt{2}-1-2}{\sqrt{2}+2}+\dfrac{\sqrt{2}+1}{\sqrt{2}}=\dfrac{\sqrt{2}-3}{\sqrt{2}+2}+\dfrac{\sqrt{2}+1}{\sqrt{2}}=\dfrac{\sqrt{2}-3+2+1+2\sqrt{2}}{\sqrt{2}\left(1+\sqrt{2}\right)}=\dfrac{3\sqrt{2}}{\sqrt{2}\left(1+\sqrt{2}\right)}=\dfrac{3}{1+\sqrt{2}}\)c)\(\dfrac{2+\sqrt{5}}{\sqrt{2}+\sqrt{3+\sqrt{5}}}+\dfrac{2-\sqrt{5}}{\sqrt{2}-\sqrt{3-\sqrt{5}}}=\dfrac{\sqrt{2}\left(2+\sqrt{5}\right)}{\left(\sqrt{2}+\sqrt{3+\sqrt{5}}\right)\sqrt{2}}+\dfrac{\sqrt{2}\left(2-\sqrt{5}\right)}{\sqrt{2}\left(\sqrt{2}-\sqrt{3-\sqrt{5}}\right)}=\dfrac{2\sqrt{2}+\sqrt{10}}{2+\sqrt{6+2\sqrt{5}}}+\dfrac{2\sqrt{2}-\sqrt{10}}{2-\sqrt{6-2\sqrt{5}}}=\dfrac{2\sqrt{2}+\sqrt{10}}{2+\sqrt{\left(\sqrt{5}+1\right)^2}}+\dfrac{2\sqrt{2}-\sqrt{10}}{2-\sqrt{\left(\sqrt{5}-1\right)^2}}=\dfrac{\sqrt{2}\left(2+\sqrt{5}\right)}{2+\sqrt{5}+1}+\dfrac{\sqrt{2}\left(2-\sqrt{5}\right)}{2-\sqrt{5}+1}=\dfrac{\sqrt{2}\left(2+\sqrt{5}\right)}{3+\sqrt{5}}+\dfrac{\sqrt{2}\left(2-\sqrt{5}\right)}{3-\sqrt{5}}=\dfrac{\sqrt{2}\left(2+\sqrt{5}\right)\left(3-\sqrt{5}\right)+\sqrt{2}\left(2-\sqrt{5}\right)\left(3+\sqrt{5}\right)}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}=\dfrac{\sqrt{2}\left(6-2\sqrt{5}+3\sqrt{5}-5+6+2\sqrt{5}-3\sqrt{5}-5\right)}{9-5}=\dfrac{2\sqrt{2}}{4}=\dfrac{1}{\sqrt{2}}\)
Làm nốt nè :3
\(2.a.P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x}=\dfrac{x-1}{x}\left(x>0;x\ne1\right)\)\(b.P>\dfrac{1}{2}\Leftrightarrow\dfrac{x-1}{x}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{x-2}{2x}>0\)
\(\Leftrightarrow x-2>0\left(do:x>0\right)\)
\(\Leftrightarrow x>2\)
\(3.a.A=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{a-\sqrt{a}}\right):\dfrac{\sqrt{a}+1}{a-1}=\dfrac{\sqrt{a}-1}{\sqrt{a}-1}.\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}=\sqrt{a}-1\left(a>0;a\ne1\right)\)
\(b.Để:A< 0\Leftrightarrow\sqrt{a}-1< 0\Leftrightarrow a< 1\)
Kết hợp với DKXĐ : \(0< a< 1\)
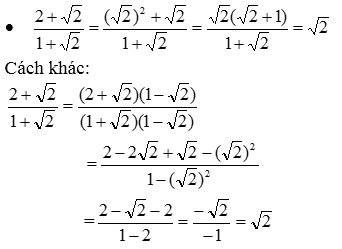
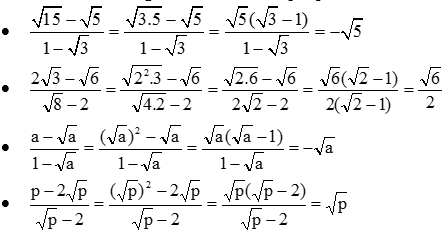
\(A=\sqrt{2}+\dfrac{1}{\sqrt{3}-1}=\sqrt{2}+\dfrac{\sqrt{3}+1}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(=\sqrt{2}+\dfrac{\sqrt{3}+1}{2}=\dfrac{2\sqrt{2}+\sqrt{3}+1}{2}\)