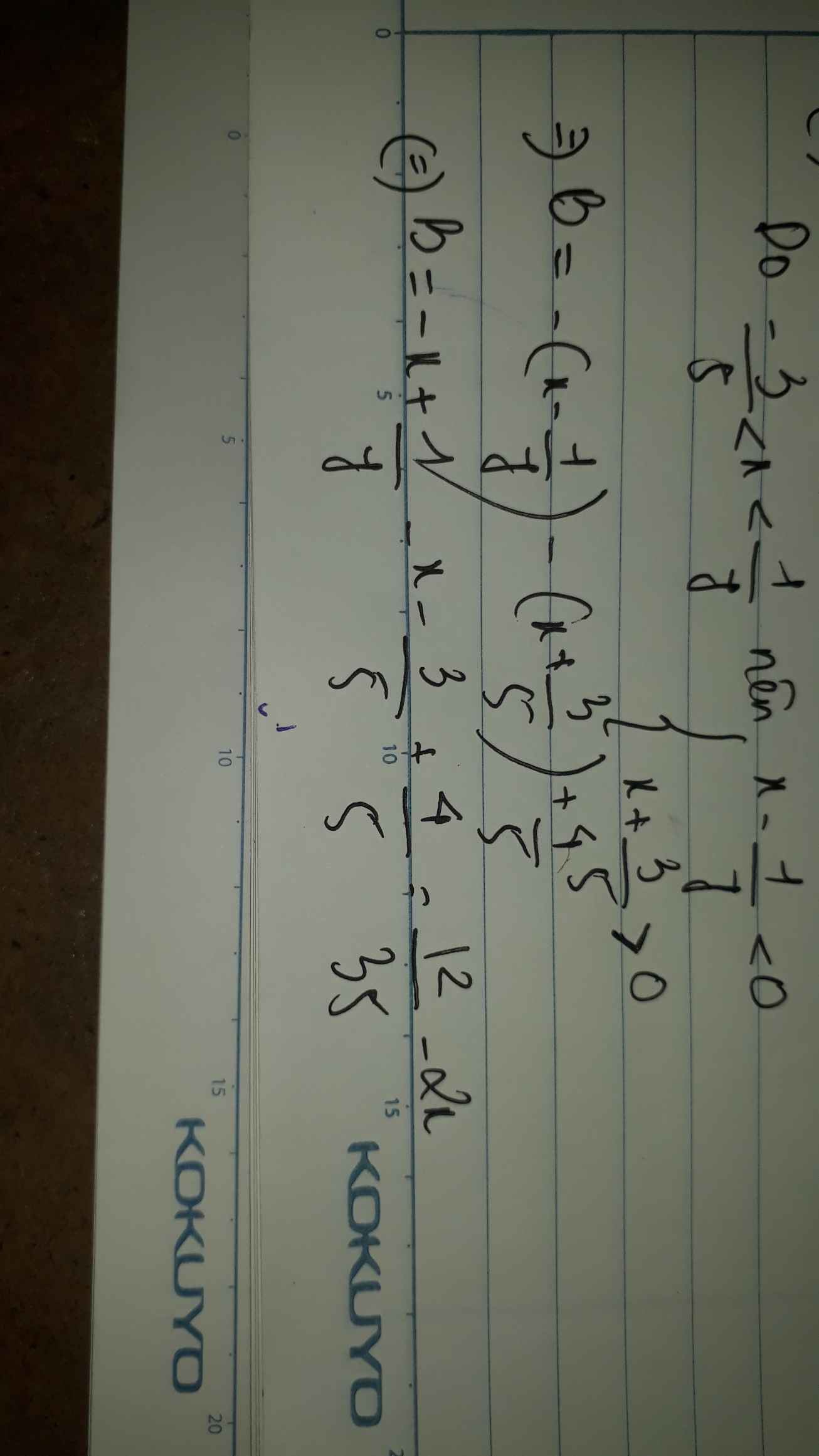Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


B = 2(3x - 1) - |5 - x|
B = 6x - 2 - 5 - x
B = (6x - x) + (-2 + 5)
B = 5x - 7


A=|3x+1|-x-2 (1)
Ta có:|3x+1|=3x+1<=>3x+1 \(\ge\) 0<=>\(x\ge-\frac{1}{3}\)
|3x+1|=-(3x+1)<=>3x+1<0\(\Leftrightarrow x<-\frac{1}{3}\)
Nếu \(x\ge-\frac{1}{3}\) thì (1) trở thành : 3x+1-x-2=(3x-x)+(1-2)=2x-1
Nếu \(x<-\frac{1}{3}\) thì (1) trở thành :-(3x+1)-x-2=-3x-1-x-2=(-3x-x)+(-1-2)=-4x-3
Vậy..............



a) với x>=5 => E=3x+1+x-5=4x-4=4(x-1)
b) th1: x<-1 => E=-x-1-x+3=-2x+2=-2(x-1)
th2: \(-1\le x\le3\)=> E=x+1-x+3=4
th3: x>3 =>E= x+1+x-3=2x-2=2(x-1)

Ta có: \(B=\left|x-\dfrac{1}{7}\right|-\left|x+\dfrac{3}{5}\right|+\dfrac{4}{5}\)
\(=-x+\dfrac{1}{7}-x-\dfrac{3}{5}+\dfrac{4}{5}\)
\(=-2x+\dfrac{12}{35}\)