
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hihi mình cũng học lớp 9, để mình giúp cậu nha!
a) \(\sqrt{3-2\sqrt{2}}+\sqrt{9+4\sqrt{2}}=\sqrt{\left(\sqrt{2}-1\right)^2}+\sqrt{\left(1+\sqrt{8}\right)^2}\)
\(=\left|\sqrt{2}-1\right|+\left|1+\sqrt{8}\right|=\sqrt{2}-1+1+\sqrt{8}=\sqrt{2}+2\sqrt{2}=3\sqrt{2}\)
b) \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(1+\sqrt{7}\right)^2}\)
\(=\left|\sqrt{7}-1\right|-\left|1+\sqrt{7}\right|=\sqrt{7}-1-1-\sqrt{7}=-2\)
c) \(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}=\sqrt{\left(\sqrt{2}+3\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=\left|\sqrt{2}+3\right|-\left|3-\sqrt{2}\right|=\sqrt{2}+3-3+\sqrt{2}=2\sqrt{2}\)
(Nhớ click cho mình với nhoa!)


`c)root{3}{4}.root{3}{1-sqrt3}.root{6}{(sqrt3+1)^2}`
`=root{3}{4(1-sqrt3)}.root{3}{1+sqrt3}`
`=root{3}{4(1-sqrt3)(1+sqrt3)}`
`=root{3}{4(1-3)}=-2`
`d)2/(root{3}{3}-1)-4/(root{9}-root{3}{3}+1)`
`=(2(root{3}{9}+root{3}{3}+1))/(3-1)-(4(root{3}{3}+1))/(3+1)`
`=root{3}{9}+root{3}{3}+1-root{3}{3}-1`
`=root{3}{9}`
`a)root{3}{8sqrt5-16}.root{3}{8sqrt5+16}`
`=root{3}{(8sqrt5-16)(8sqrt5+16)}`
`=root{3}{320-256}`
`=root{3}{64}=4`
`b)root{3}{7-5sqrt2}-root{6}{8}`
`=root{3}{1-3.sqrt{2}+3.2.1-2sqrt2}-root{6}{(2)^3}`
`=root{3}{(1-sqrt2)^3}-sqrt2`
`=1-sqrt2-sqrt2=1-2sqrt2`

\(A=-\sqrt{2}-\sqrt{1}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+....-\sqrt{7}-\sqrt{8}+\sqrt{8}+\sqrt{9}\)
\(A=\sqrt{9}-\sqrt{1}=3-1=2\)


với n >0, ta có :
\(\left(\sqrt{n+1}+\sqrt{n}\right)\left(\sqrt{n+1}-\sqrt{n}\right)=n+1-n=1\Rightarrow\frac{1}{\sqrt{n+1}-\sqrt{n}}=\sqrt{n+1}+\sqrt{n}\)
Gọi biểu thức đã cho là A
\(A=\frac{1}{-\left(\sqrt{2}-\sqrt{1}\right)}-\frac{1}{-\left(\sqrt{3}-\sqrt{2}\right)}+...+\frac{1}{-\left(\sqrt{8}-\sqrt{7}\right)}-\frac{1}{-\left(\sqrt{9}-\sqrt{8}\right)}\)
\(A=-\frac{1}{\sqrt{2}-\sqrt{1}}+\frac{1}{\sqrt{3}-\sqrt{2}}-...-\frac{1}{\sqrt{8}-\sqrt{7}}+\frac{1}{\sqrt{9}-\sqrt{8}}\)
\(A=-\left(\sqrt{2}+\sqrt{1}\right)+\left(\sqrt{3}+\sqrt{2}\right)-...-\left(\sqrt{8}+\sqrt{7}\right)+\left(\sqrt{9}+\sqrt{8}\right)\)
\(A=-\sqrt{1}+\sqrt{9}=2\)
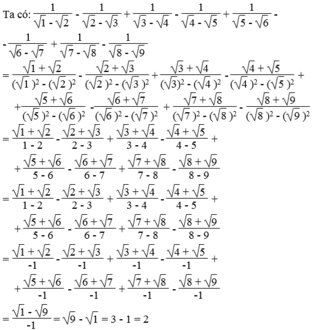
\(\sqrt{8-4\sqrt{3}}=\sqrt{6-2.\sqrt{6}.\sqrt{2}+2}=\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}=\left|\sqrt{6}-\sqrt{2}\right|=\sqrt{6}-\sqrt{2}\)
\(\sqrt{9-6\sqrt{2}}=\sqrt{6-2\sqrt{6}.\sqrt{3}+3}=\sqrt{\left(\sqrt{6}-\sqrt{3}\right)^2}=\left|\sqrt{6}-\sqrt{3}\right|=\sqrt{6}-\sqrt{3}\)
\(\sqrt{8-4\sqrt{3}}=\sqrt{6}-\sqrt{2}\)
\(\sqrt{9-6\sqrt{2}}=\sqrt{6}-\sqrt{3}\)