NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 2 2022
a: \(\dfrac{-7}{x^2-4}=\dfrac{-7}{\left(x-2\right)\left(x+2\right)}=\dfrac{-14}{2\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{11}{2x+4}=\dfrac{11}{2\left(x+2\right)}=\dfrac{11\left(x-2\right)}{2\left(x+2\right)\left(x-2\right)}\)
b: \(\dfrac{2}{9x^2-1}=\dfrac{2}{\left(3x-1\right)\left(3x+1\right)}\)
\(\dfrac{4x}{1-3x}=\dfrac{-4x}{3x-1}=\dfrac{-4x\left(3x+1\right)}{\left(3x-1\right)\left(3x+1\right)}\)
c: \(\dfrac{3}{x+2}=\dfrac{6\left(x^2-2x+4\right)}{2\left(x+2\right)\left(x^2-2x+4\right)}\)
\(\dfrac{x+1}{x^3+8}=\dfrac{2x+2}{2\left(x+1\right)\left(x^2-2x+4\right)}\)
\(\dfrac{x+2}{2\left(x+2\right)}=\dfrac{\left(x+2\right)\left(x^2-2x+4\right)}{2\left(x+2\right)\left(x^2-2x+4\right)}\)
PN
25 tháng 11 2015
\(a.\) Ta có:
\(MTC:\) \(\left(x+1\right)\left(x+2\right)\)
Do đó
\(\frac{3x}{x+1}=\frac{3x\left(x+2\right)}{\left(x+1\right)\left(x+2\right)}\)
\(\frac{x+4}{x+2}=\frac{\left(x+1\right)\left(x+4\right)}{\left(x+1\right)\left(x+2\right)}\)
\(b.\) Ta có:
\(x^2+x=x\left(x+1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
nên \(MTC:\) \(x\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\frac{5}{x^2+x}=\frac{5}{x\left(x+1\right)}=\frac{5\left(x-1\right)}{x\left(x-1\right)\left(x+1\right)}\)
\(\frac{6}{x^2-1}=\frac{6}{\left(x-1\right)\left(x+1\right)}=\frac{6x}{x\left(x-1\right)\left(x+1\right)}\)
\(c.\) Ta có:
\(x^2-5x+4=x^2-x-4x+4=x\left(x-1\right)-4\left(x-1\right)=\left(x-1\right)\left(x-4\right)\)
\(2x^2-8x=2x\left(x-4\right)\)
nên \(MTC:\) \(2x\left(x-1\right)\left(x-4\right)\)
Do đó:
\(\frac{4}{x^2-5x+4}=\frac{4}{\left(x-1\right)\left(x-4\right)}=\frac{8x}{2x\left(x-1\right)\left(x-4\right)}\)
\(\frac{x+1}{2x^2-8x}=\frac{x+1}{2x\left(x-4\right)}=\frac{\left(x-1\right)\left(x+1\right)}{2x\left(x-1\right)\left(x-4\right)}\)
27 tháng 11 2020
Làm nốt d :P
\(\frac{x+3}{2x^2-15x-8};\frac{3}{x^2-8x}\)
Ta có : \(2x^2-15x-8=\left(2x+1\right)\left(x-8\right)\)
\(x^2-8x=x\left(x-8\right)\)
MTC : \(x\left(x-8\right)\left(2x+1\right)\)
\(\frac{x+3}{2x^2-15x-8}=\frac{x+3}{\left(2x+1\right)\left(x-8\right)}=\frac{x^2+3x}{x\left(x-8\right)\left(2x+1\right)}\)
\(\frac{3}{x^2-8x}=\frac{3}{x\left(x-8\right)}=\frac{6x+3}{x\left(x-8\right)\left(2x+1\right)}\)
24 tháng 7 2017
a) \(\dfrac{3x}{2x+4}\) và \(\dfrac{x+3}{x^2-4}\)
Phân tích các mẫu thức thành nhân tử :
\(2x+4 = 2(x+2)\)
\(x^2 - 4 = (x-2)(x+2)\)
MTC : \(2(x+2)(x-2)\)
Nhân tử phụ của mẫu thức : \(2x + 4\) là \((x - 2)\)
\(x^2 - 4\) là \(2\)
QĐ: \(\dfrac{3x}{2x+4}=\dfrac{3x}{2\left(x+2\right)}=\dfrac{3x\left(x-2\right)}{2\left(x+2\right)\left(x-2\right)}\)
\(\dfrac{x+3}{x^2-4}=\dfrac{x+3}{\left(x+2\right)\left(x-2\right)}=\dfrac{2\left(x+3\right)}{2\left(x+2\right)\left(x-2\right)}\)
b) \(\dfrac{x+5}{x^2+4x+4}\) và \(\dfrac{x}{3x+6}\)
Phân tích các mẫu thức thành nhân tử :
\(x^2+4x+4 = (x+2)^2\)
\(3x + 6\) \(= 3(x+2)\)
MTC : \(3(x+2)^2\)
Nhân tử phụ của mẫu thức : \(x^2 + 4x +4 \) là \(3\)
\(3x + 6\) là \((x+2)\)
QĐ : \(\dfrac{x+5}{x^2+4x+4}=\dfrac{\left(x+5\right)}{\left(x+2\right)^2}=\dfrac{3\left(x+5\right)}{3\left(x+2\right)^2}\)
\(\dfrac{x}{3x+6}=\dfrac{x}{3\left(x+2\right)}=\dfrac{x\left(x+2\right)}{3\left(x+2\right)^2}\)
27 tháng 12 2015
a,\(\frac{2x^2+4x}{x+2}\)=\(\frac{2x\left(x+2\right)}{x+2}\)\(=2x\)
b, \(\frac{3x}{2x+4}\)=\(\frac{3x^2-6x}{2\left(x+2\right)\left(x-2\right)}\)
\(\frac{x+3}{x^2+4}\)=\(\frac{2x+6}{2\left(x-2\right)\left(x+2\right)}\)
tick mình nhé!!
TD
1
27 tháng 11 2020
\(\frac{10}{x+2};\frac{5}{2x-4};\frac{1}{6-3x}\)
Ta có : \(x+2=x+2\)
\(2x-4=2\left(x-2\right)\)
\(6-3x=3\left(2-x\right)=-3\left(x-2\right)\)
MTC : \(-6\left(x-2\right)\left(x+2\right)\)
\(\frac{10}{x+2}=\frac{10.\left(-6\right)\left(x-2\right)}{-6\left(x-2\right)\left(x+2\right)}=\frac{-60x+120}{-6\left(x-2\right)\left(x+2\right)}\)
\(\frac{5}{2x-4}=\frac{5}{2\left(x-2\right)}=\frac{5.\left(-3\right)\left(x+2\right)}{-6\left(x-2\right)\left(x+2\right)}=\frac{-15x-30x}{-6\left(x-2\right)\left(x+2\right)}\)
\(\frac{1}{6-3x}=\frac{1}{-3\left(x-2\right)}=\frac{2\left(x+2\right)}{-6\left(x-2\right)\left(x+2\right)}=\frac{2x+4}{-6\left(x-2\right)\left(x+2\right)}\)
PN
16 tháng 5 2021
\(x-5=\frac{1}{3\left(x+2\right)}\left(đkxđ:x\ne-2\right)\)
\(< =>3\left(x-5\right)\left(x+2\right)=1\)
\(< =>3\left(x^2-3x-10\right)=1\)
\(< =>x^2-3x-10=\frac{1}{3}\)
\(< =>x^2-3x-\frac{31}{3}=0\)
giải pt bậc 2 dễ r
PN
16 tháng 5 2021
\(\frac{x}{3}+\frac{x}{4}=\frac{x}{5}-\frac{x}{6}\)
\(< =>\frac{4x+3x}{12}=\frac{6x-5x}{30}\)
\(< =>\frac{7x}{12}=\frac{x}{30}< =>12x=210x\)
\(< =>x\left(210-12\right)=0< =>x=0\)
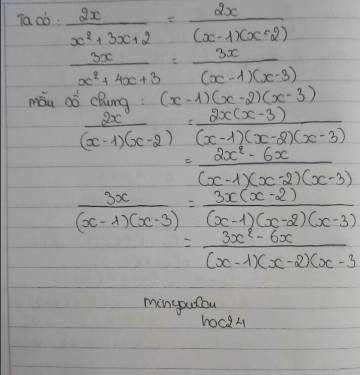
\(\frac{3x}{2x+4}=\frac{3x\left(x-2\right)}{2\left(x+2\right)\left(x-2\right)}=\frac{3x^2-6x}{2\left(x+2\right)\left(x-2\right)}=\)
\(\frac{x+3}{x^2-4}=\frac{2\left(x+3\right)}{2\left(x+2\right)\left(x-2\right)}=\frac{2x+6}{2\left(x+2\right)\left(x-2\right)}\)
`(3x)/(2x+4)`
`= (3x (x-2) )/( (2x+4) (x-2) )`
`= (3x^2 - 6x)/(2 (x+2) (x-2) )`
`(x+3)/(x^2 - 4)`
`= (x+3)/(x^2 - 2^2)`
`= (x+3)/( (x-2) (x+2) )`
`= (2 (x+3) )/(2 (x-2) (x+2) )`
`= (2x+ 6)/(2 (x+2) (x-2) )`