Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

a) \(\dfrac{3}{8}\) và \(\dfrac{5}{27}\)
Mẫu số chung là 216
Quy đồng:
\(\dfrac{3.27}{8.27}\)=\(\dfrac{81}{216}\) ; \(\dfrac{5.8}{27.8}\)=\(\dfrac{40}{216}\)
b)\(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\)
Mẫu số chung là:225
Quy đồng:
\(\dfrac{-2.25}{9.25}\)=\(\dfrac{-50}{225}\) ; \(\dfrac{4.9}{25.9}\)=\(\dfrac{36}{225}\)
c)\(\dfrac{1}{15}\) và -6
Mẫu số chung là 15
Quy đồng:
\(\dfrac{1}{15}\) ;\(\dfrac{-6.15}{15}\)=\(\dfrac{-90}{15}\)

a: 2/9=4/18
1/3=6/18
5/18=5/18
b: 7/15=14/30
1/5=6/30
-5/6=-25/30
c: -21/56=-3/7
-3/16=-63/336
5/24=70/336
-21/56=-3/7=-144/336
d: \(\dfrac{-4}{7}=\dfrac{-36}{63}\)
8/9=56/63
\(-\dfrac{10}{21}=-\dfrac{30}{63}\)
e: 3/-20=-3/20=-9/60
-11/-30=11/30=22/60
7/15=28/60

a: 7/30=21/90
8/45=16/90
11/90=11/90
b: -4/5=-168/210
1/6=35/210
-9/7=-270/210
c: -7/24=-21/72
11/12=66/72
-23/36=-46/72
d: 17/30=85/150
-22/75=-44/150
5=750/150

b: \(C=\left(\dfrac{12}{199}+\dfrac{23}{200}-\dfrac{34}{201}\right)\cdot\dfrac{3-2-1}{6}=0\)

a;\(\dfrac{-6}{11}\) : \(\dfrac{12}{55}\) = \(\dfrac{-5}{2}\)
b;\(\dfrac{7}{12}\) + \(\dfrac{5}{72}\) - \(\dfrac{11}{36}\) = \(\dfrac{47}{72}\) - \(\dfrac{11}{36}\) = \(\dfrac{25}{72}\)
c;\(\dfrac{13}{10}\) : \(\dfrac{-5}{13}\) = \(\dfrac{-169}{50}\)
d; {\(\dfrac{5}{12}\) + \(\dfrac{5}{11}\) } : { \(\dfrac{5}{3}\) -\(\dfrac{7}{11}\) } = \(\dfrac{115}{132}\) : \(\dfrac{34}{33}\) = \(\dfrac{115}{136}\)
lưu ý mk ko chép đầu bài
mình cần gấp lắm đến chiều mai là phải nộp rùi
giúp mình nha thanks cá bạn trước ![]() ko có tâm trạng mà cười nữa
ko có tâm trạng mà cười nữa![]()
![]()

a: \(\dfrac{25\cdot9-25\cdot17}{-8\cdot80-8\cdot10}=\dfrac{25\cdot\left(-8\right)}{\left(-8\right)\cdot\left(80+10\right)}=\dfrac{25}{90}=\dfrac{5}{18}=\dfrac{250}{900}\)
\(\dfrac{48\cdot12-48\cdot15}{\left(-3\right)\cdot\left(270+30\right)}=\dfrac{48}{300}=\dfrac{8}{50}=\dfrac{144}{900}\)
\(\dfrac{2^5\cdot3}{600}=\dfrac{96}{600}=\dfrac{144}{900}\)
b: \(\dfrac{2^5\cdot7+25}{25\cdot5^2-2^5\cdot3}=\dfrac{32\cdot7+25}{25\cdot25-32\cdot3}=\dfrac{249}{529}=\dfrac{1743}{7\cdot529}\)
\(\dfrac{3^4\cdot5-3^6}{3^4\cdot13+3^4}=\dfrac{3^4\left(5-9\right)}{3^4\left(13+1\right)}=\dfrac{-4}{14}=\dfrac{-2}{7}=\dfrac{-1058}{7\cdot529}\)


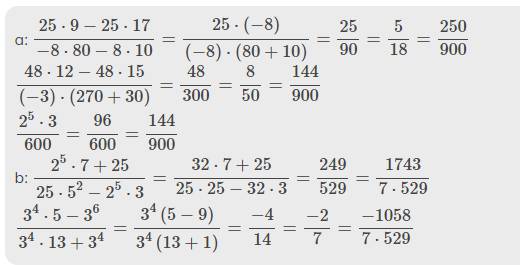
\(\dfrac{1}{2}+\dfrac{2}{4}\\ \dfrac{2}{4}=\dfrac{1\cdot2}{2\cdot2}=\dfrac{2}{4}\\ \dfrac{3}{-12}+\dfrac{4}{12}\\ \dfrac{3}{-12}=\dfrac{-3}{12}\\ \dfrac{4}{6}=\dfrac{4\cdot2}{6\cdot2}=\dfrac{8}{12}\\ \dfrac{-3}{12}+\dfrac{8}{13}=\dfrac{5}{12}\)
\(\dfrac{8}{13}?\)