NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PN
25 tháng 11 2015
\(a.\) Ta có:
\(MTC:\) \(\left(x+1\right)\left(x+2\right)\)
Do đó
\(\frac{3x}{x+1}=\frac{3x\left(x+2\right)}{\left(x+1\right)\left(x+2\right)}\)
\(\frac{x+4}{x+2}=\frac{\left(x+1\right)\left(x+4\right)}{\left(x+1\right)\left(x+2\right)}\)
\(b.\) Ta có:
\(x^2+x=x\left(x+1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
nên \(MTC:\) \(x\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\frac{5}{x^2+x}=\frac{5}{x\left(x+1\right)}=\frac{5\left(x-1\right)}{x\left(x-1\right)\left(x+1\right)}\)
\(\frac{6}{x^2-1}=\frac{6}{\left(x-1\right)\left(x+1\right)}=\frac{6x}{x\left(x-1\right)\left(x+1\right)}\)
\(c.\) Ta có:
\(x^2-5x+4=x^2-x-4x+4=x\left(x-1\right)-4\left(x-1\right)=\left(x-1\right)\left(x-4\right)\)
\(2x^2-8x=2x\left(x-4\right)\)
nên \(MTC:\) \(2x\left(x-1\right)\left(x-4\right)\)
Do đó:
\(\frac{4}{x^2-5x+4}=\frac{4}{\left(x-1\right)\left(x-4\right)}=\frac{8x}{2x\left(x-1\right)\left(x-4\right)}\)
\(\frac{x+1}{2x^2-8x}=\frac{x+1}{2x\left(x-4\right)}=\frac{\left(x-1\right)\left(x+1\right)}{2x\left(x-1\right)\left(x-4\right)}\)
27 tháng 11 2020
Làm nốt d :P
\(\frac{x+3}{2x^2-15x-8};\frac{3}{x^2-8x}\)
Ta có : \(2x^2-15x-8=\left(2x+1\right)\left(x-8\right)\)
\(x^2-8x=x\left(x-8\right)\)
MTC : \(x\left(x-8\right)\left(2x+1\right)\)
\(\frac{x+3}{2x^2-15x-8}=\frac{x+3}{\left(2x+1\right)\left(x-8\right)}=\frac{x^2+3x}{x\left(x-8\right)\left(2x+1\right)}\)
\(\frac{3}{x^2-8x}=\frac{3}{x\left(x-8\right)}=\frac{6x+3}{x\left(x-8\right)\left(2x+1\right)}\)
29 tháng 7 2021
cho mình hỏi là giữa khác phân số với nhua là phải có dấu như là công, trừ, nhân hay chia chứ?
M
1
28 tháng 7 2023
\(\dfrac{x^2-4}{x^2+2x}=\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x+2\right)}=\dfrac{x-2}{x}=\dfrac{\left(x-2\right)^2}{x\left(x-2\right)}\)
\(\dfrac{x}{x-2}=\dfrac{x^2}{x\left(x-2\right)}\)
H9
HT.Phong (9A5)
CTVHS
29 tháng 9 2023
a) \(\dfrac{1}{x^3-8}=\dfrac{1}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{2}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
\(\dfrac{3}{4-2x}=\dfrac{-3}{2\left(x-2\right)}=\dfrac{-3\left(x^2+2x+4\right)}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
b) \(\dfrac{x}{x^2-1}=\dfrac{x}{\left(x+1\right)\left(x-1\right)}=\dfrac{x\left(x+1\right)}{\left(x+1\right)^2\left(x-1\right)}\)
\(\dfrac{1}{x^2+2x+1}=\dfrac{1}{\left(x+1\right)^2}=\dfrac{x-1}{\left(x+1\right)^2\left(x-1\right)}\)
c) \(\dfrac{1}{x+2}=\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{1}{x^2-4x+4}=\dfrac{1}{\left(x-2\right)^2}=\dfrac{x+2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{5}{2-x}=\dfrac{-5}{x-2}=\dfrac{-5\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)^2}\)
d) \(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{\left(x-y\right)^2}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{2x}{x^2-y^2}=\dfrac{2x}{\left(x+y\right)\left(x-y\right)}=\dfrac{6x\left(x-y\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{x^2-xy+y^2}{x^2-2xy+y^2}=\dfrac{x^2-xy+y^2}{\left(x-y\right)^2}=\dfrac{3\left(x^2-xy+y^2\right)\left(x+y\right)}{3\left(x+y\right)\left(x-y\right)^2}=\dfrac{3\left(x^3+y^3\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
27 tháng 12 2015
a,\(\frac{2x^2+4x}{x+2}\)=\(\frac{2x\left(x+2\right)}{x+2}\)\(=2x\)
b, \(\frac{3x}{2x+4}\)=\(\frac{3x^2-6x}{2\left(x+2\right)\left(x-2\right)}\)
\(\frac{x+3}{x^2+4}\)=\(\frac{2x+6}{2\left(x-2\right)\left(x+2\right)}\)
tick mình nhé!!
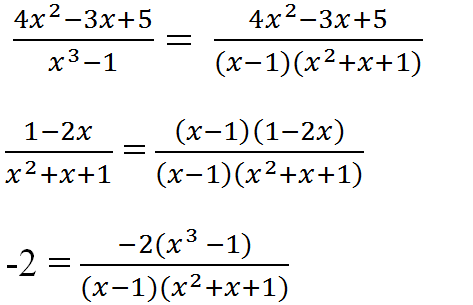
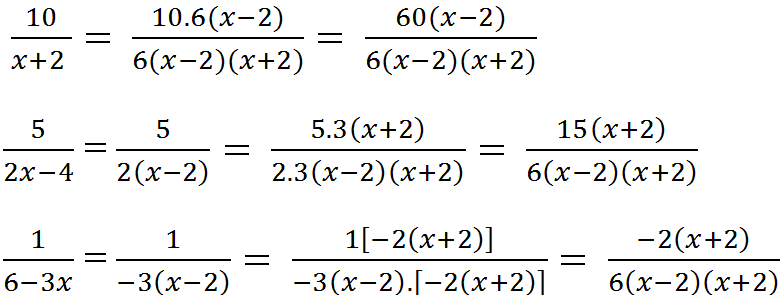
Lời giải:
$\frac{2x+3}{4-x^2}=\frac{-(2x+3)}{x^2-4}=\frac{-(2x+3)}{(x-2)(x+2)}=\frac{-(2x+3)(x-2)}{(x-2)^2(x+2)}=\frac{-(2x^2-x-6)}{(x-2)^2(x+2)}$
$\frac{5x-4}{x^2-4x+4}=\frac{(5x-4)(x+2)}{(x^2-4x+4)(x+2)}=\frac{5x^2+6x-8}{(x-2)^2(x+2)}$