Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

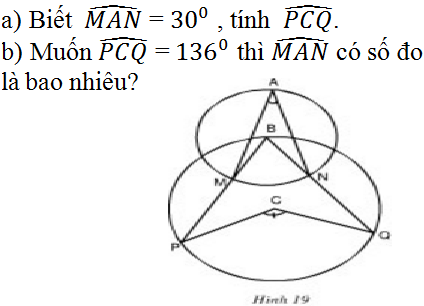
a)Ta có: \(\widehat{MAN}\)=\(\frac{1}{2}\)sđcung MN(góc nội tiếp chắn cung MN)
và \(\widehat{MBN}\)=sđcung MN (góc ở tâm chắn cung MN)
\(\Rightarrow\)\(\widehat{MAN}=\frac{1}{2}\)\(\widehat{MBN}\)=30
=>\(\widehat{MBN}\)=60
Ta lại có:\(\widehat{MBN}=\frac{1}{2}\)sđ cung PQ(góc nội tiếp chắn cung PQ)
và \(\widehat{PCQ}\)= sđ cung PQ(góc ở tâm chắn cung PQ)
=> \(\widehat{MBN}=\frac{1}{2}\widehat{PCQ}\)=60
=>\(\widehat{PCQ}\)= 120
b) Ta có:\(\widehat{MBN}=\frac{1}{2}\widehat{PCQ}\)(cmt)
mà \(\widehat{PCQ}\)=136 (gt)
=>\(\widehat{MBN}\)=68
mà \(\widehat{MAN}=\frac{1}{2}\widehat{MBN}\) (cmt)
=>\(\widehat{MAN}\)=34


Phương trình 5x2 + 2x -16 =0 có hệ số a=5 ,b=2 c=-16
Ta có: Δ'=12 -5(-16) = 1 + 80 =81 >0
Δ' = 81 =9
Phương trình 3x2 -2x -5 =0 có hệ số a =3,b = -2, c = -5
Ta có: Δ'=(-1)2 -3(-5) = 1 + 15 =16 >0
Δ' = 16 =4
Phương trình 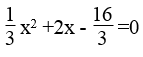
Δ'=32 -1(-16) = 9 +16 =25 > 0
Δ' = 25 =5
Phương trình 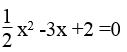
Ta có: Δ'=(-3)2 -1.4 = 9 -4 =5 >0
Δ' = 5

Ba điểm không thẳng hàng sẽ tạo thành một tam giác. Để đường tròn qua hết 3 điểm đó thì đường tròn đó sẽ là đường tròn ngoại tiếp của tam giác.
Vì 3 điểm chỉ tạo nên 1 tam giác cho nên tam giác cúng chỉ có 1 đường tròn ngoại tiếp duy nhất.
Kết luận: chỉ có 1.

a) \(P=\left(\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}-\frac{2}{4-x}\right):\frac{\sqrt{x}+3}{\sqrt{x}-2}\left(ĐK:x\ge0;x\ne4\right)\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)+\sqrt{x}-2+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}-2}{\sqrt{x}+3}\)
\(=\frac{x+2\sqrt{x}+\sqrt{x}}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}=\frac{\sqrt{x}}{\sqrt{x}+2}\)
b) Vì: \(\sqrt{x}+4>0,\forall x\inĐK\)
=> \(2\sqrt{x}+4>\sqrt{x}\)
=> \(\frac{\sqrt{x}}{2\sqrt{x}+4}< 0\)
=> \(\frac{\sqrt{x}}{\sqrt{x}+2}< 2\)
=>đpcm
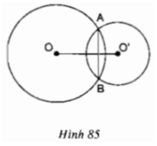

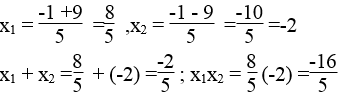
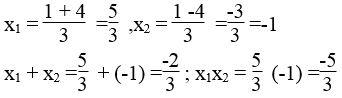
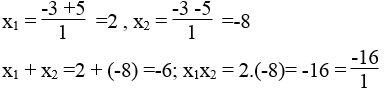
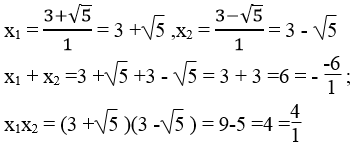

Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB