Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

khi đ1 và đ2 sáng bt thì
I = I đm = I1đm + I2đm ( 2 cái I này bạn tính ở từng đèn )
⇔ \(\dfrac{U}{R_{tđ}}\)= I đm = I1đm + I2đm
⇔\(\dfrac{U}{R_1+\dfrac{R_{đ2}.R_{đ1}}{R_{đ2}+R_{đ1}}}\) = I1đm + I2đm
thế số vô => R1

a) Cơ năng trong quá trình dao động là:
W=\(\frac{1}{2}\)mω2A2=\(\frac{1}{2}\).0,2.202.52=1000(J)
b) Biểu thức thế năng là:
Wt=\(\frac{1}{2}\)mω2A2cos2(ωt+φ0)= \(\frac{1}{2}\).0,2.202.52cos2(20t)=1000cos2(20t)
Biểu thức động năng là:
Wd=\(\frac{1}{2}\)mω2A2sin2(ωt+φ0)= \(\frac{1}{2}\).0,2.202.52sin2(20t)=1000sin2(20t)

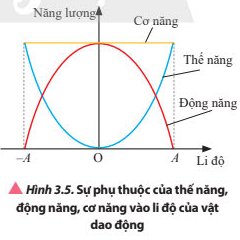
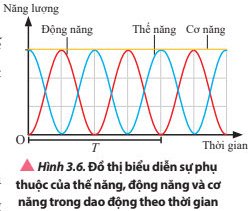
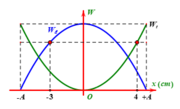
Vật chuyển động từ biên âm về vị trí cân bằng thì thế năng của vật giảm từ giá trí lớn nhất về 0 còn động năng thì tăng dần từ 0 đến giá trị lớn nhất và ngược lại.
Vật chuyển động từ vị trí cân bằng đến vị trí biên âm thì thế năng của vật tăng dần từ 0 đến giá trị lớn nhất còn động năng giảm dần từ giá trị lớn nhất về 0 và ngược lại.






 Tìm cường độ dòng điện qua các điện trở và số chỉ của ampe kế? Bỏ qua điện trở của ampe kế.
Tìm cường độ dòng điện qua các điện trở và số chỉ của ampe kế? Bỏ qua điện trở của ampe kế.

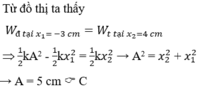
Khi thế năng của vật tăng thì động năng của vật giảm và cơ năng luôn bằng tổng giá trị của động năng và thế năng .