Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

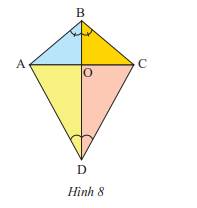
a) Tia BO là tia phân giác của \(\widehat {ABC}\) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.
Tia DO là tia phân giác của \(\widehat {ADC}\) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau
b) Vì BO là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABO} = \widehat {CBO} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.100^\circ = 50^\circ \)
Vì DO là tia phân giác của \(\widehat {ADC}\)nên \(\widehat {ADO} = \widehat {CDO} = \frac{1}{2}.\widehat {ADC} = \frac{1}{2}.60^\circ = 30^\circ \)
Vậy \(\widehat {ABO} = 50^\circ ;\widehat {ADO} = 30^\circ \)

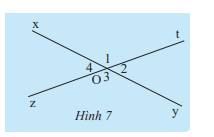
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh

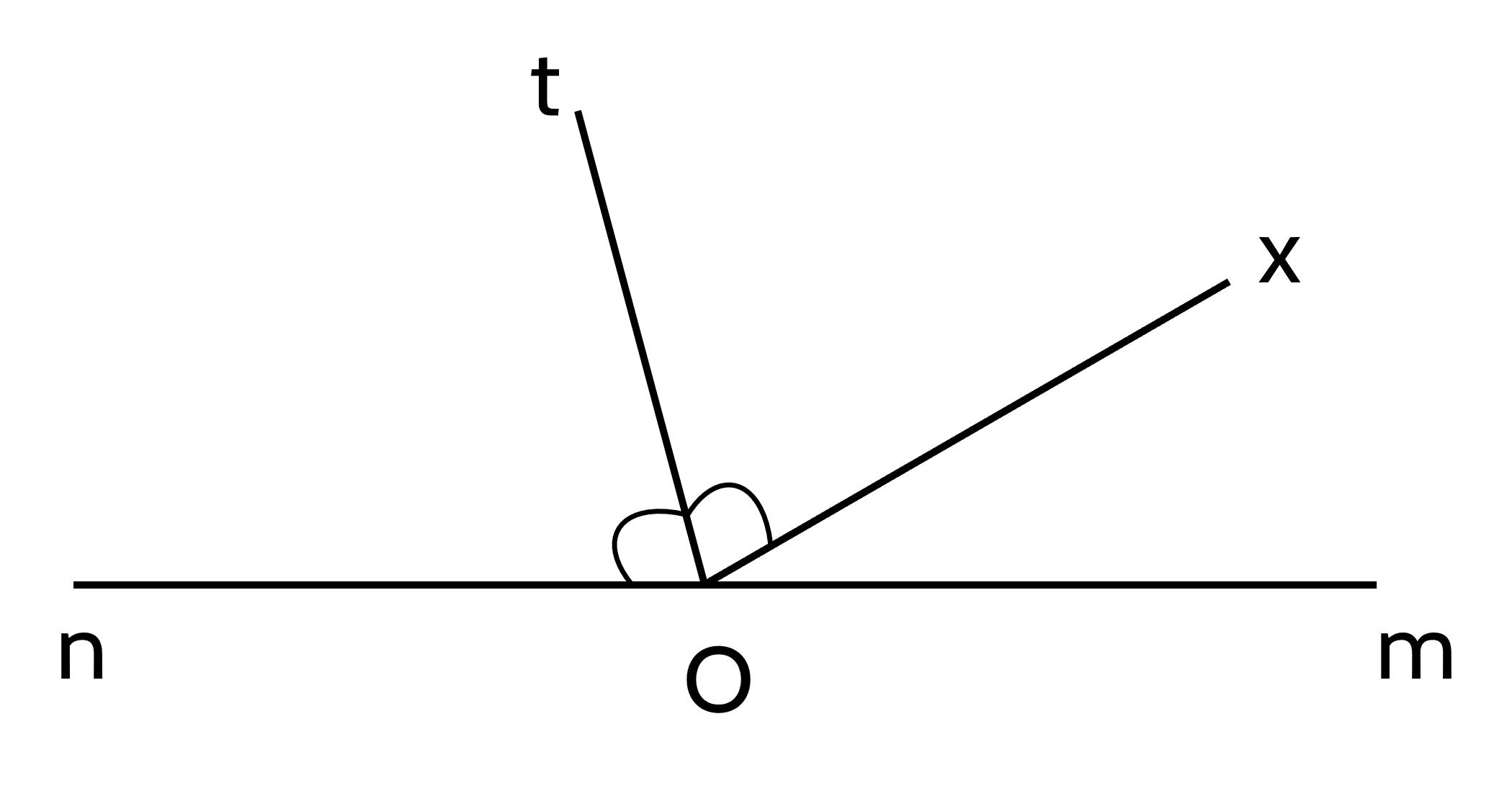
2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

a) Ta có:
∠mOx + ∠nOx = 180⁰ (kề bù)
⇒ ∠nOx = 180⁰ - ∠mOx
= 180⁰ - 30⁰
= 150⁰
Do Ot là tia phân giác của ∠nOx
⇒ ∠nOt = ∠nOx : 2
= 150⁰ : 2
= 75⁰
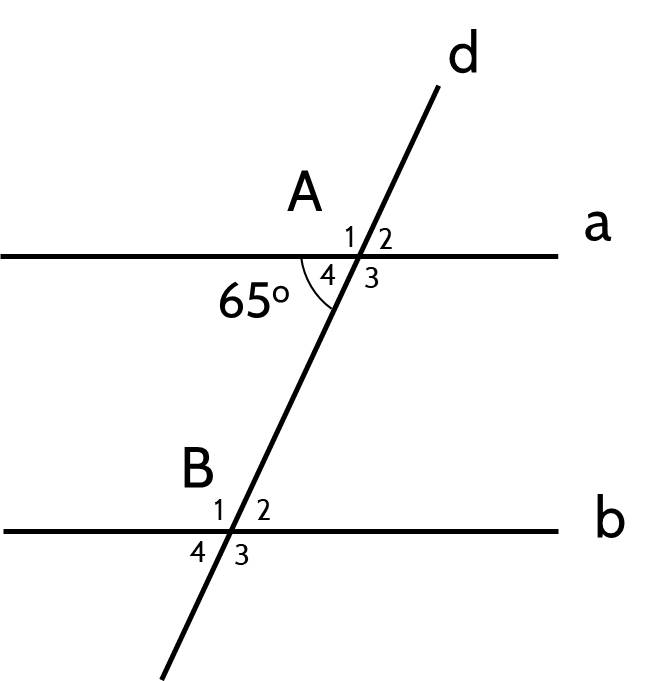
b) Do a // b
⇒ ∠B₄ = ∠A₄ = 65⁰ (đồng vị)
Ta có:
∠B₃ + ∠B₄ = 180⁰ (kề bù)
⇒ ∠B₃ = 180⁰ - ∠B₄
= 180⁰ - 65⁰
= 115⁰
Tính số đo góc �3^B3.
Hướng dẫn giải:a) ���^+���^=180∘mOx+xOn=180∘
Vậy ���^=180∘−30∘=150∘nOx=180∘−30∘=150∘.
��Ot là tia phân giác của ���^nOx, suy ra ���^=12.���^=75∘nOt=21.nOx=75∘.
b) a // b suy ra �4^=�2^=65∘A4=B2=65

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
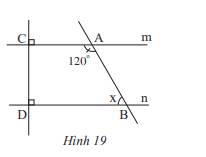






a) Vì m và n cùng vuông góc với CD nên m // n
b) Ta có: \(\widehat {{A_2}} + \widehat {{A_1}} = 180^\circ \Rightarrow 120^\circ + \widehat {{A_1}} = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - 120^\circ = 60^\circ \)
Vì m // n nên \(\widehat {{A_1}} = \widehat {ABD}\) ( 2 góc so le trong) nên \(\widehat {ABD}\) = 60\(^\circ \)
Vậy x = 60\(^\circ \)