Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)
Xét \(\Delta AIB\) và \(\Delta AIC\) có :
IB = IC ( gt )
Chung AI
\(\widehat{I_1}=\widehat{I_2}=90^0\)
=> \(\Delta AIB\) = \(\Delta AIC\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)=> AI là tia phân giác của góc BAC=> AB = ACb)C/m tương tự ta => BC = BD ; AB = AD=> AB = BC = CD = DA
a: Xét ΔABC có
AI là đường trung tuyến
AI là đường cao
Do đó: ΔABC cân tại A
hay AI là tia phân giác của góc BAC
b: Xét tứ giác ABDC có
I là trung điểm của AD
I là trung điểm của BC
Do đó: ABDC là hình bình hành
mà AB=AC
nên ABDC là hình thoi
=>AB=AC=CD=DB
a: Xét ΔABC có
AI là đường trung tuyến
AI là đường cao
Do đó: ΔABC cân tại A
hay AI là tia phân giác của góc BAC
a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đối đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
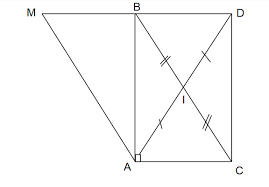
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM
Bạn ơi, vì mình k thể kí hiệu góc. Nên bạn tự ghi góc vào bài làm của mình nhé
a: Xét ΔBID và ΔCIA có
IB=IC
\(\widehat{BID}=\widehat{CIA}\)
ID=IA
Do đó: ΔBID=ΔCIA
b: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: BD\(\perp\)AB
Em tham khảo nhé!
Câu hỏi của Vy Hà Khánh - Toán lớp 7 - Học toán với OnlineMath
Cm: a) Xét t/giác ABI và t/giác ACI
có: AI : chung
\(\widehat{AIB}=\widehat{AIC}=90^0\) (gt)
BI = CI (gt)
=> t/giác ABI = t/giác ACI (c.g.c)
=> \(\widehat{BAI}=\widehat{CAI}\) (2 góc t/ứng)
=> AI là tia p/giác của góc BAC
b) Xét t/giác AIB và t/giác DIC
có: AI = DI (gt)
\(\widehat{AIB}=\widehat{CID}\) (đối đỉnh)
BI = CI (gt)
=> t/giác AIB = t/giác DIC (c.g.c)
=> AB = CD (2 cạnh t/ứng) (1)
Xét t/giác AIC và t/giác DIB
có: AI = ID (gt)
\(\widehat{AIC}=\widehat{BID}\) (đối đỉnh)
IC = IB (gt)
=> t/giác AIC = t/giác DIC (c.g.c)
=> AC = BD (2 cạnh t/ứng) (2)
Mà AB = AC (vì t/giác AIB = t/giác AIC) (3)
Từ (1); (2) và (3) => AB = AC = CD = DB