Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: góc OBA+góc OCA=90+90=180 độ
=>OBAC nội tiếp
Xét ΔCME và ΔBMC có
góc M chung
góc CEM=góc BCM
=>ΔCME đồng dạng với ΔBMC
b: Xét ΔABE và ΔAKB có
góc ABE=góc AKB
góc BAE chung
=>ΔABE đồng dạng với ΔAKB
=>BF/BK=BA/AK=AE/AB
Xét ΔACE và ΔAKC có
góc ACE=góc AKC
góc CAE chung
=>ΔACE đồng dạng với ΔAKC
=>CE/CK=AE/AC
=>CE/CK=BF/BK
=>CE*BK=CF*BK
b) Ta thấy (O) giao (I) tại 2 điểm B và D => BD vuông góc OI (tại K) => ^OKB=900.
Xét đường tròn (I) đường kính AB có H thuộc cung AB => AH vuông góc HB hay AH vuông góc BC (1)
AB và AC là 2 tiếp tuyến của (O) => \(\Delta\)ABC cân tại A. Mà AO là phân giác ^BAC
=> AO vuông góc BC (2)
Từ (1) và (2) => A;H;O thẳng hàng => ^OHB=900.
Xét tứ giác BOHK: ^OKB=^OHB=900 => Tứ giác BOHK nội tiếp đường tròn đường kính OB
=> ^OKH = ^OBH. Lại có ^OBH=^OAB (Cùng phụ ^HBA) => ^OKH = ^OAB
Hay ^OKH = ^HAI. Mà ^OKH + ^KHI = 1800 nên ^HAI + ^KHI = 1800
=> Tứ giác AIKH nội tiếp đường tròn (đpcm).
b) Dễ thấy OI là trung trực của BD và OI cắt BD tại K => K là trung điểm của BD
\(\Delta\)ABC cân đỉnh A có đường phân giác AH => H là trung điểm BC
Từ đó suy ra HK là đường trung bình của \(\Delta\)BDC
=> HK//CD => ^HKD + ^CDK = 1800 (3). Đồng thời \(\frac{HK}{CD}=\frac{1}{2}\)
Tương tự KI là đường trg bình của \(\Delta\)BAD => KI//AD => ^DKI + ^ADK = 1800 (4) Và \(\frac{IK}{AD}=\frac{1}{2}\)
Cộng (3) với (4) => ^KHD + ^KDI + ^CDK + ^ ADK = 3600
<=> ^HKI = 3600 - (^CDK + ^ADK) => ^HKI = ^CDA.
Xét \(\Delta\)HKI và \(\Delta\)CDA: ^HKI=^CDA; \(\frac{HK}{CD}=\frac{IK}{AD}=\frac{1}{2}\)=> \(\Delta\)HKI ~ \(\Delta\)CDA (c.g.c)
=> ^HIK = ^CAD. Mặt khác: ^CAD = ^DBE (Cùng chắn cung DE) => ^HIK=^DBE.
Mà tứ giác AIKH nội tiếp đường tròn => ^HIK=^HAK = >^DBE=^HAK hay ^KBF=^FAK
=> Tứ giác BKFA nội tiếp đường tròn => Đường tròn ngoại tiếp tam giác ABF đi qua điểm K (đpcm).
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
A B O ^ = 90 0 A C O ^ = 90 0 A B O ^ + A C O ^ = 180 0
=> tứ giác ABOC nội tiếp được đường tròn.
b) Vẽ cát tuyến ADE của (O) sao cho ADE nằm giữa 2 tia AO, AB; D, E Î (O) và D nằm giữa A, E. Chứng minh A B 2 = A D . A E .
Tam giác ADB đồng dạng với tam giác ABE
⇒ A B A E = A D A B ⇔ A B 2 = A D . A E
c) Gọi F là điểm đối xứng của D qua AO, H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
Ta có D H A ^ = E H O ^
nên D H A ^ = E H O ^ = A H F ^ ⇒ A H E ^ + A H F ^ = 180 0 ⇒ 3 điểm E, F, H thẳng hàng.
Có 1 phần câu trả lời ở đây.
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube
a.Vì AB là tiếp tuyến của (O)
\(\Rightarrow MB\) là tiếp tuyến của (O)
\(\Rightarrow\widehat{MBI}=\widehat{BCM}\)
\(\Rightarrow\Delta MBI~\Delta MCB\left(g.g\right)\)
b ) Từ câu a ) \(\Rightarrow\frac{MB}{MC}=\frac{MI}{MB}\Rightarrow MB^2=MI.MC\)
Mà M là trung điểm AB \(\Rightarrow MA=MB\Rightarrow MA^2=MI.MC\)
\(\Rightarrow\frac{MA}{MI}=\frac{MC}{MA}\Rightarrow\Delta MAI~\Delta MCA\left(c.g.c\right)\)
c ) Từ câu a , b \(\Rightarrow\widehat{MBI}=\widehat{MCI},\widehat{MAI}=\widehat{ACI}\)
\(\Rightarrow\widehat{BCD}=\widehat{BID}=\widehat{IBA}+\widehat{IAB}=\widehat{ICB}+\widehat{ICA}=\widehat{BCA}=\widehat{BDC}\)
\(\Rightarrow\Delta BCD\) cân tại B
1) Ta có \(\widehat{ABO}=\widehat{ACO}=90độ\left(gt\right)\)
Do đó\(\widehat{ABO}+\widehat{ACO}=180độ\)
Nên tứ giác ABOC nội tiếp đường tròn đường kính AO
Tâm đường tròn ngoại tiếp tứ giác ABOC là trung điểm AO.
2) Xét ΔABD và ΔAEB có
\(\widehat{BAE}\)chung
\(\widehat{ABD}=\widehat{AEB}\)(góc tạo bởi tia tiếp tuyến và dây và góc nội tiếp cùng chắn \(\widebat{BD}\))
Nên ΔABD 
Do đó \(\frac{AB}{AE}\)=\(\frac{AD}{AB}\)
Hay AB2= AE.AD
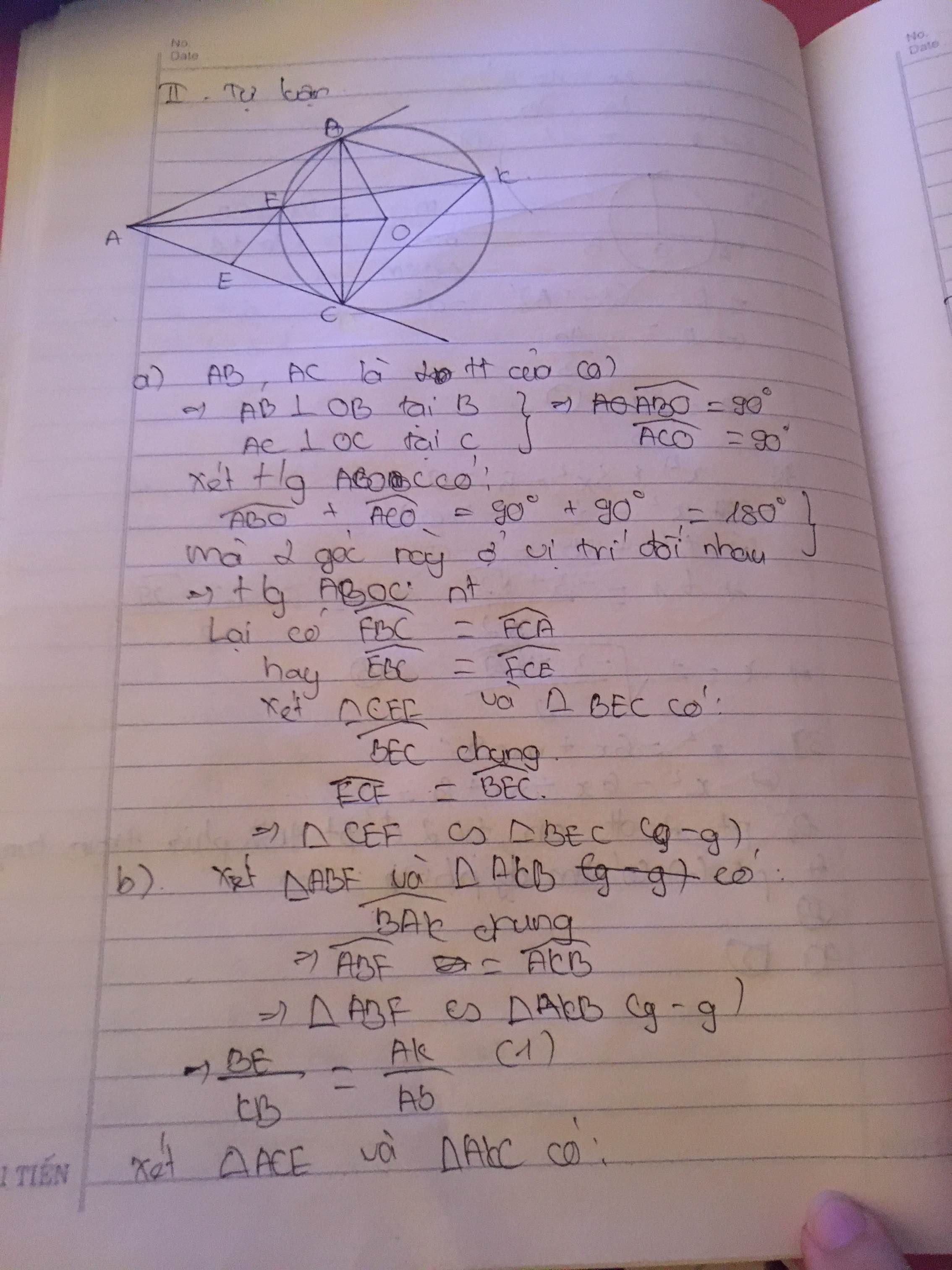
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp